Electricity, Electromagnetism and the LICOSAS
This article explores what the geometry of the LICOSAS might offer in understanding electricity and electromagnetism. As with several of the other articles in this series, we ask what if? What if the geometry we call the Licosas could tell us about the nature of these? Again, I must give the standard caveat, these are my mental meanderings and not standard science. LICOSAS is an acronym for a geometric sequence that runs Line, Cone, (circle) SAddlemniscus, Sphere. Saddlemniscus is short for saddled lemniscate meniscus. When an infinite number of degrees have been added we cover all points on a sphere. The saddlemniscus is designated as "S∞".
In spite of its mathematical underpinnings, it is easy to understand. You can model it with paper circles, adhesive tape and imagination. Basic Unit of the Universe, UU Basics ,shows you how.
We will also draw heavily upon these articles:
Force
Intermediate Unit of the Universe
The Atom
Density
In "Intermediate Unit of the Universe" we describe the different forms that an S∞ can take and how that would accommodate states of higher or lower potential. They were given the names Spiral and Ruff and their equations can be found in that article. The yellow sphere at the center represents the infinitely dense point center. The shadow sphere surrounding it represents the transitional area. This is described in the article "The Atom" where a correspondence is made with this geometry.


A new article has been added to help visualize how the series flows one into the other,
S∞ is composed of a twisted two dimensional sheet which is posited to have mass. That sheet is in turn composed of lines. We have also demonstrated in Basic UU how the Licosas series starts with a line. This line is considered the lower limit of a cone. It is the compression of the rest of the series into its simplest state. A simple analogy of the number line may help illustrate the sequence. Where the number one is the base point in the number line, the Licosas has the circle. Above one are all the numbers to infinity. Above circle are all the degrees to sphere. (Recall that the saddlemniscus adds additional degrees to a circle, until a sphere is achieved.) Below one are the reciprocals. There are also an infinite number of them, down to infinity minus one. Below circle are the degrees of cone all the way down to line. It may be argued that zero is equivalent to point, but that is for another time. Cones and circles are composed of lines. The sphere has radii pointing in all directions. So each sphere has some radius that points to any other sphere. In the article "Force" we adopt the term rail to refer to any pair of radii common to two S∞. A rail is a line, but a line with potential. The above illustrations of the spiral and ruff show a rail at the vertical axis. This is where the greatest concentration of lines occurs for the ruff as the S∞ grows. The spiral has a defined pole also but is more evenly distributed.
Let's get back to electricity. In "Force", a generalized concept of rail was introduced as a one dimensional pathway for the exchange of energy between atoms. Here we will consider the rails concentrated about the axes of the two forms. The ruff concentrates radii about its polar center. The spiral more evenly distributes radii but does have a pole also. To begin the visualization of electrical exchange, set up a line of spirals with the axes collinear. At one end is a ruff.

The ruff becomes more energized by an undetermined source. How can it pass energy along the mutual rail to the spiral? The spiral is described as a point centered helix. Under the influence of ruff's energy, it stretches into a linear helix. The difference between the equations of point centered and linear spirals is simply the multiplier to the axial component of the formula. These are modeled with parametric equations. In my current CAD system, it is the difference between cos(pi*t) vs 2*cos(pi*t).

For us to now conjure up an electrical current, assume an electrical pressure which charges the left side and a ground on the right side. The end ruff is able to transmit its form to the second position. The nature of these two forms is that they are interchangeable. Nothing is added to the veil or subtracted. Only the form transmogrifies. This allows the form of the ruff to jump to the right as the left end momentarily relaxes into a spiral. Their equations are quite similar and can be found in Intermediate UU.

This exchange of forms is not mysterious, an animation of the transmogrification is included with the Licosas Series Animated. It can be directly accessed here, The Spiral-Ruff Transition.
And so it proceeds. We allow the infamous black box to again charge the leftmost form from spiral to ruff as the ruff in the second position advances to the third and so forth.

This is my model of the passing of energy during an electrical event. Look at a line of these. If there is a source and sink, current will flow down this line as the exchange is handed from one to the next. At the end, the final ruff sinks to ground. If the source is an alternating current generator, the process will flow forward and back.

ELECTROMAGNETISM What then of electromagnetism. Examine the forms shown in Figure 8 and 9. We are still subject to the Density Difference Ratio. Neither spiral nor ruff have a limited radius. The veil, by definition, is infinite in extent. The shadowy spiral is that part which exists beyond the one atom thick wire. That is its greater envelope.
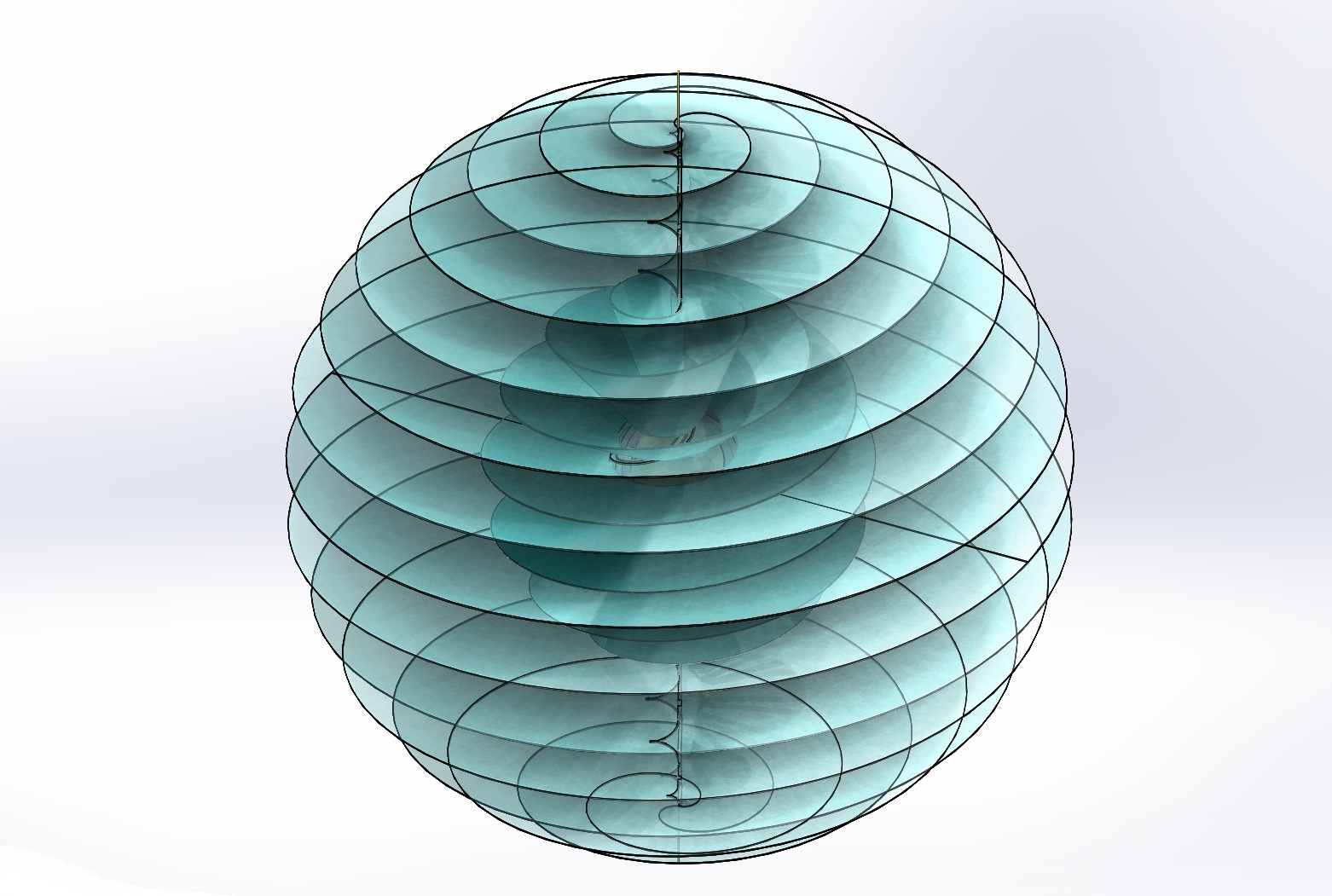
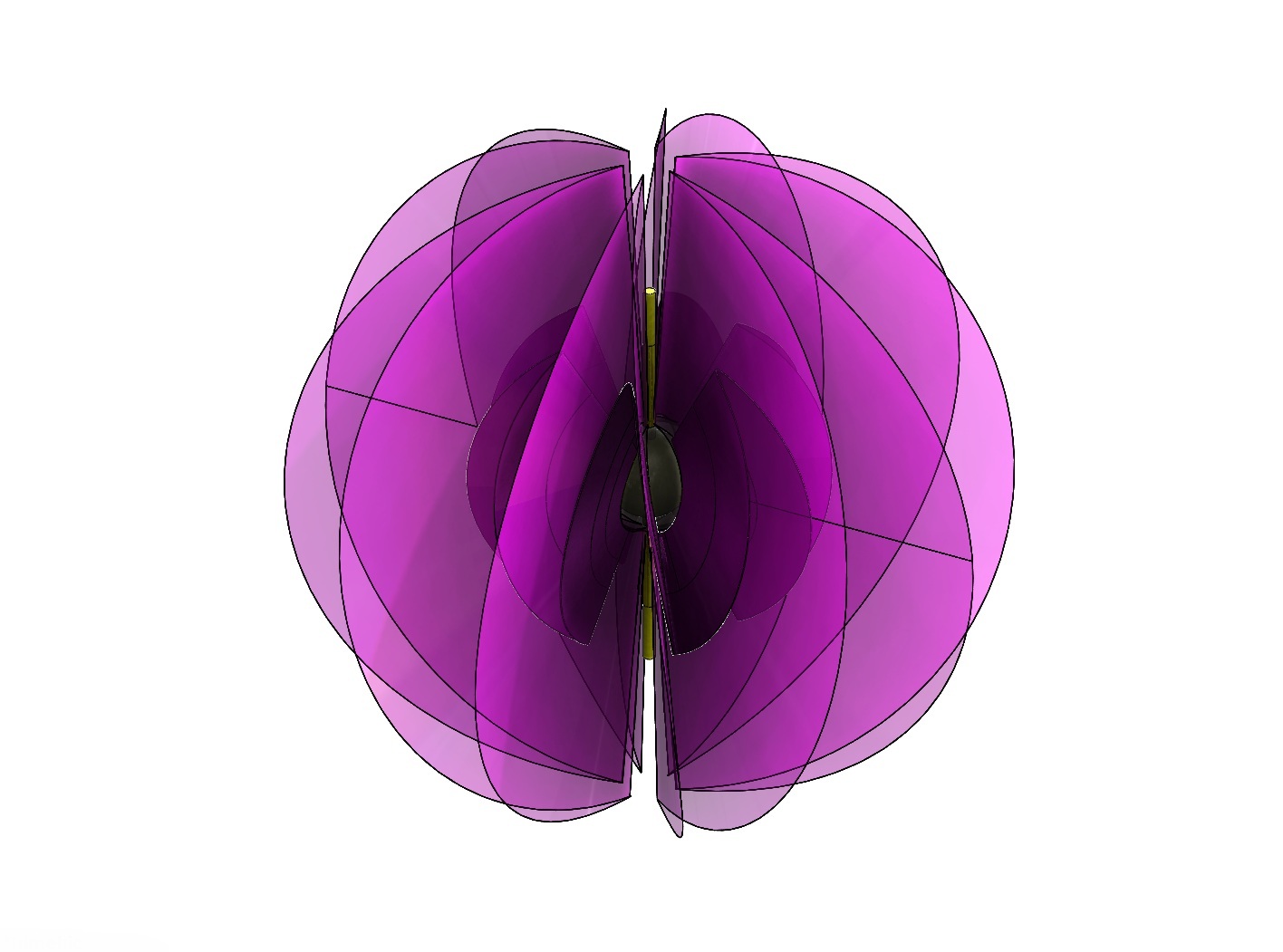
Fig. 10 indicates the extended electrical field. The blue helix represents the magnetic field using the right hand rule. Direction of current is indicated by the green arrow.
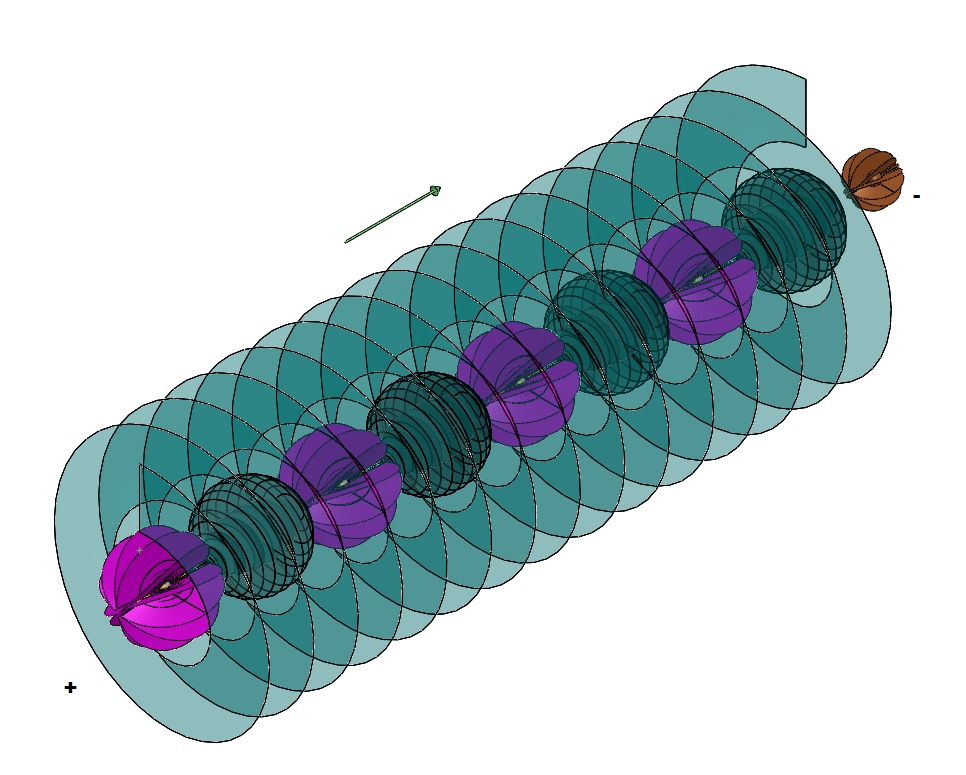
THE SOLENOID As current flows through the wire, a magnetic field is created. These ruff-spiral exchanges are happening all along the wire as electricity flows until the circuit is interrupted. As we have indicated, the ruff tends to axial concentration and the spiral is more spherically balanced. The illustration shows the spiral dominating in the radial, extended area of the field. Winding the wire into a coil creates a solenoid. As electricity flows through the solenoid, electromagnetic force is generated. That force acquires the potential to move and/or magnetize objects. Conversely, a magnet moving through a coil of wire will generate an electric current. Electromagnetism is one of the four fundamental forces. It has been investigated for centuries and is well defined by modern physics. What can our Licosas add? First, let us coil our ruff-spiral wire into a helix. In the illustrations, a red helix has been added for clarity. The green vector represents the electromagnetic field inside the coil, pointing N.

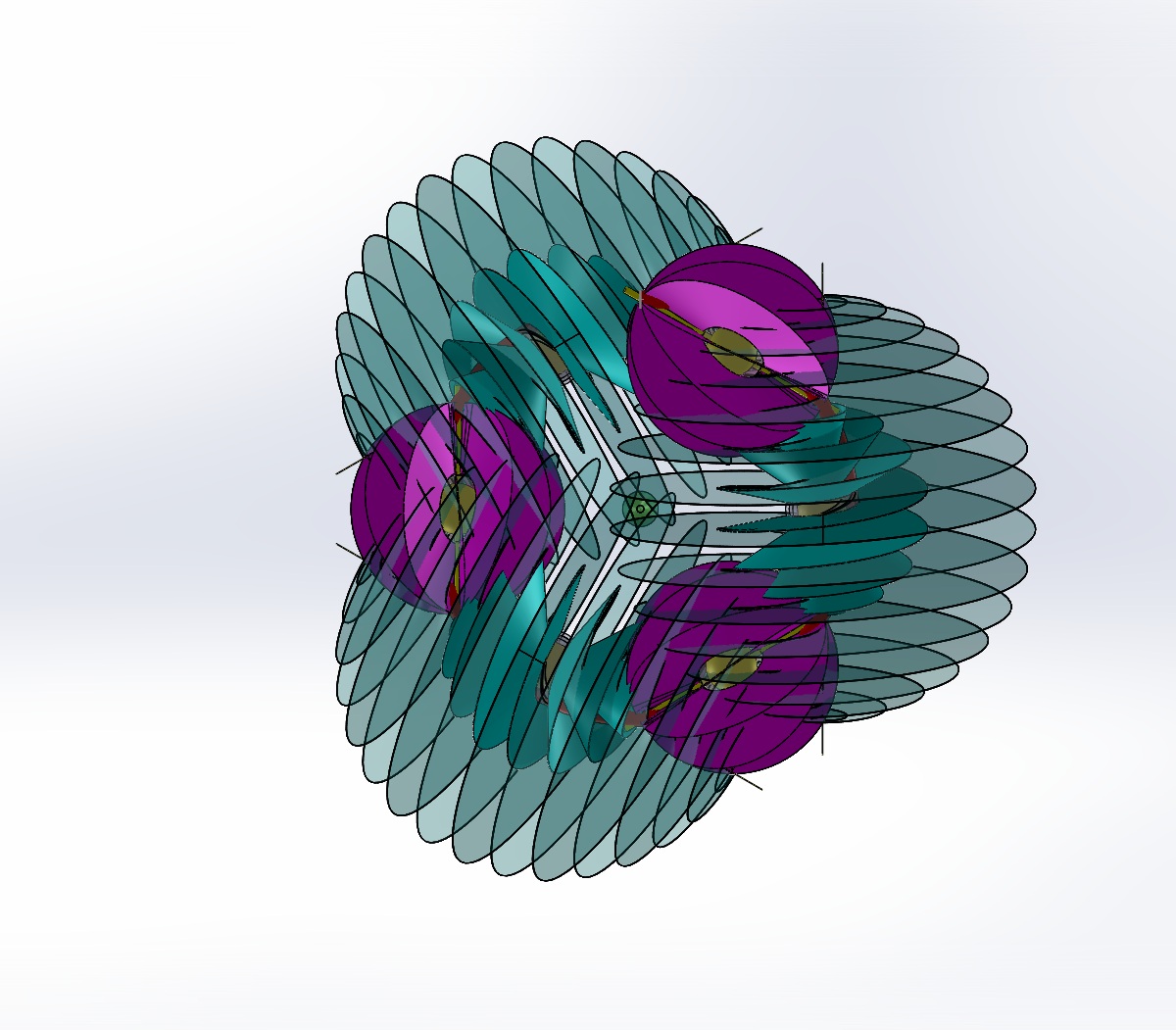
The spirals become more concentrated to the inside of the coil than the outside. So do the ruffs. The shadow veils are used to indicate that the effectiveness of the veil is reduced as the distance from the center is decreased. This is well defined as an inverse square law. The illustration is a simplification and does not refer to a specific radial distance. For this illustration there are six (6) atoms per turn of the helix. It begins at the bottom with a ruff. Next is a spiral with the larger shadow shown. This sequence is continued for the first turn, two more ruffs and larger shadow spirals. These are followed by an alternating sequence of three ruffs and two simple spirals. These were added to help make the illustration clearer. The sequence could continue on indefinitely. A real wire is more than one atom thick and the coil would be much more than one atom radius. You will have to use your imagination to extend this to larger, real world models.
The top and bottom views are shown below. The green circle in the center is the vector arrow pointing at you. The central area is much more crowded than the outside. The veils of the spirals are shown to overlap each other. In this system, veils are allowed to pass through each other but not themselves.
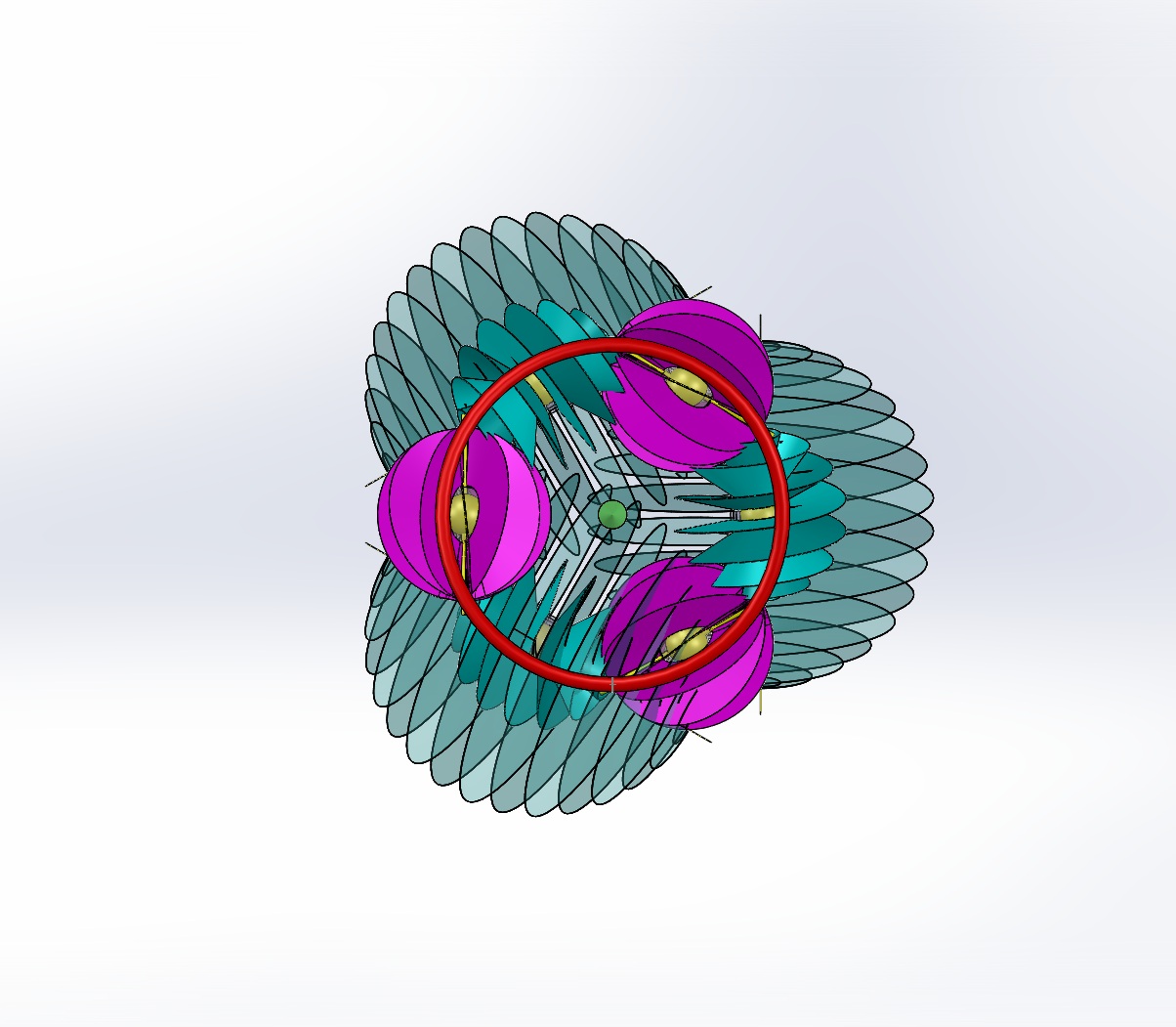
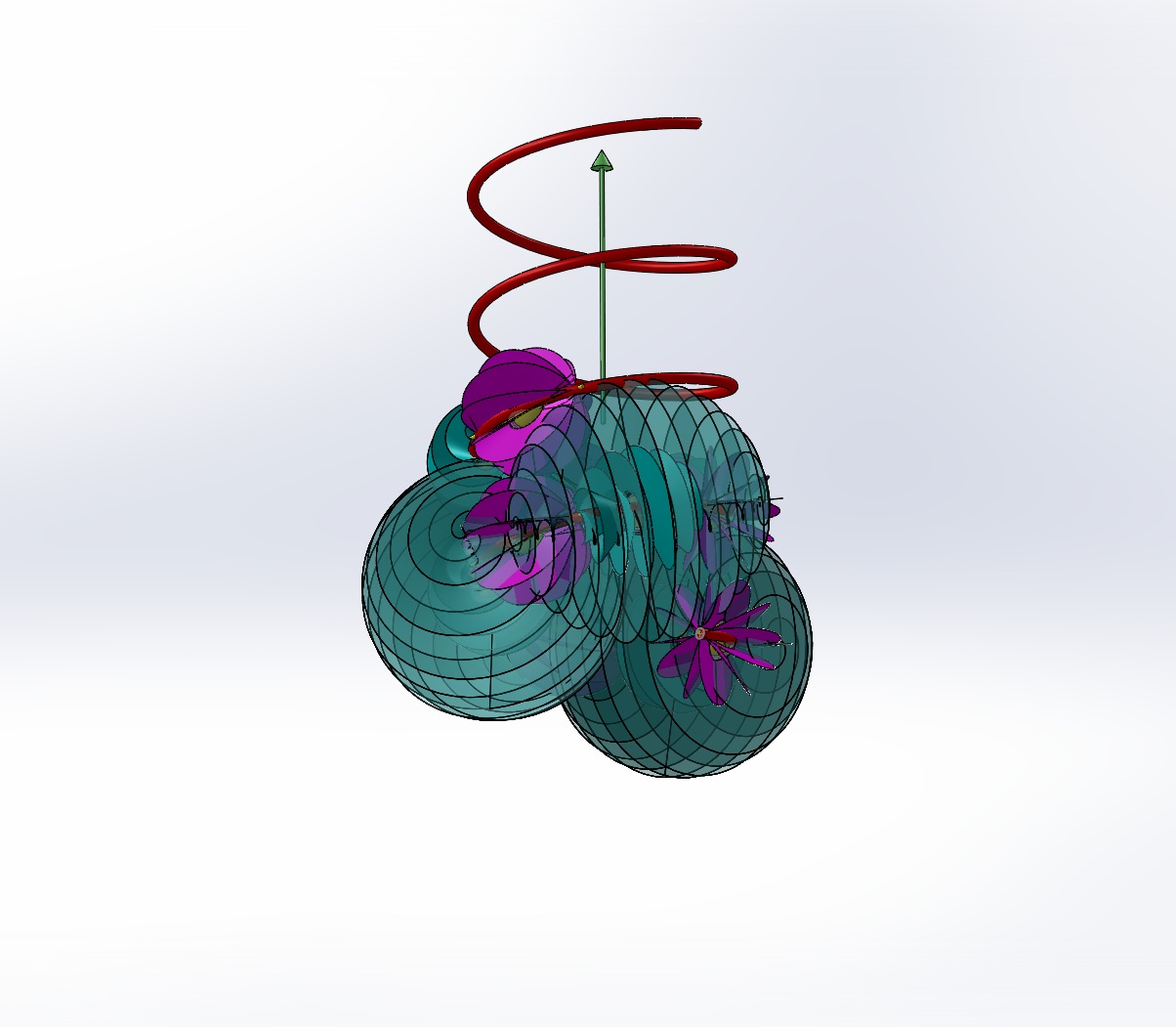
It is well known that this coil would have an electromagnetic field. Here we represent that field with a toroidal helix. A torus is a doughnut shaped object. Wrapping a coil around it produces the helix. It is like wrapping a Slinky around and connecting its ends together. The field extends from the central axis outwards. It would be better represented as a helicoid. It has been left as a linear helix to avoid obstructing the drawing.
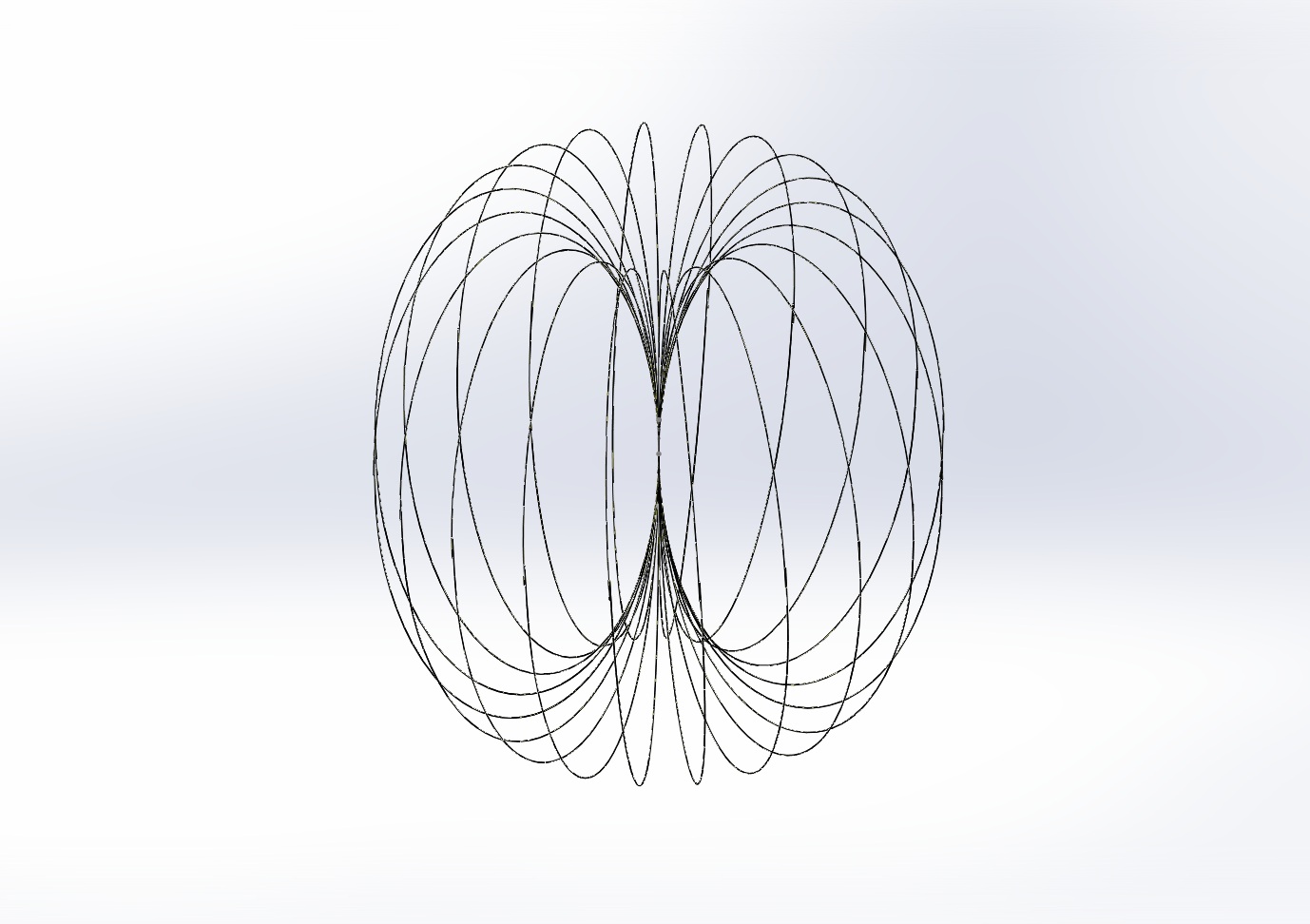
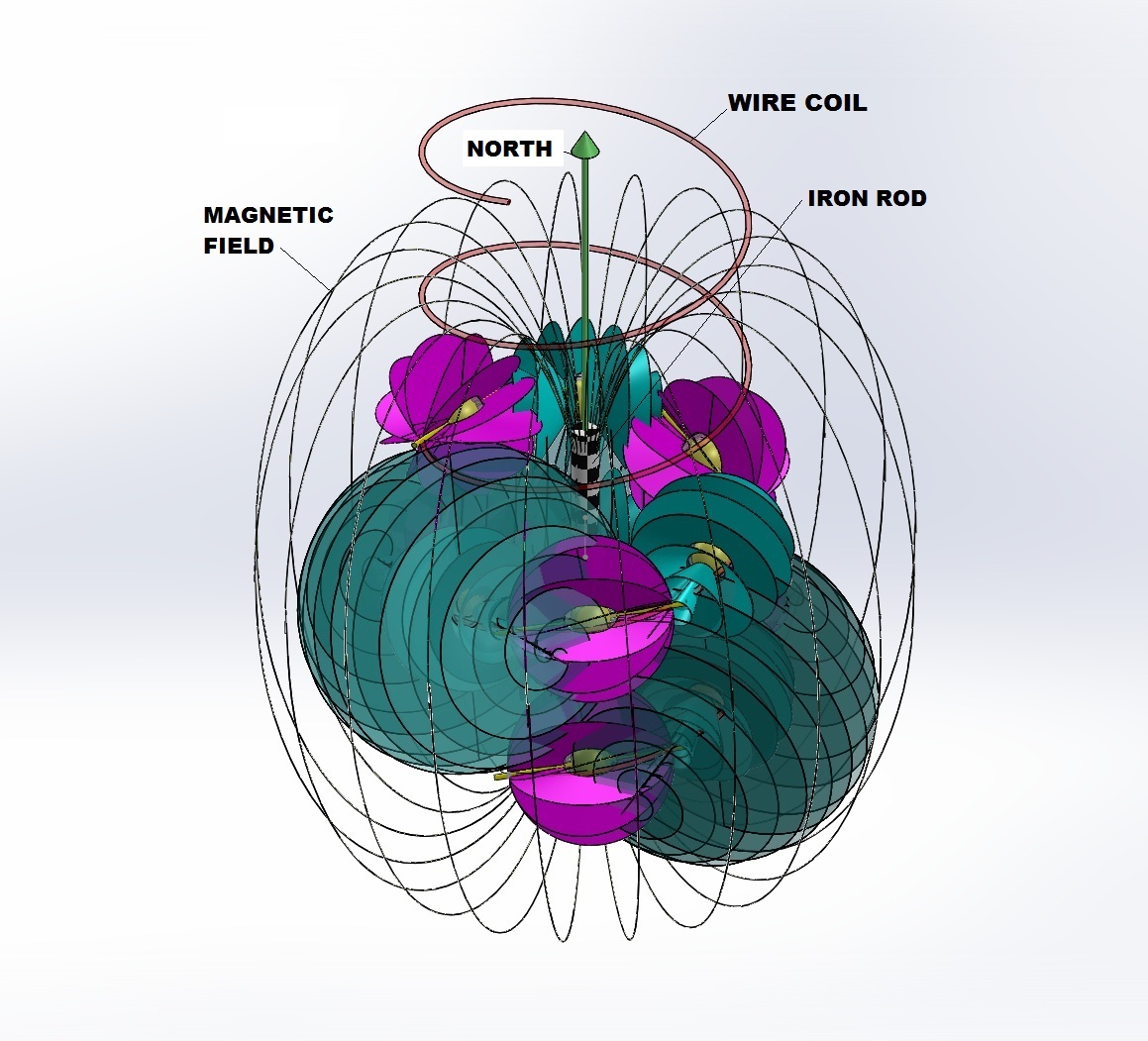
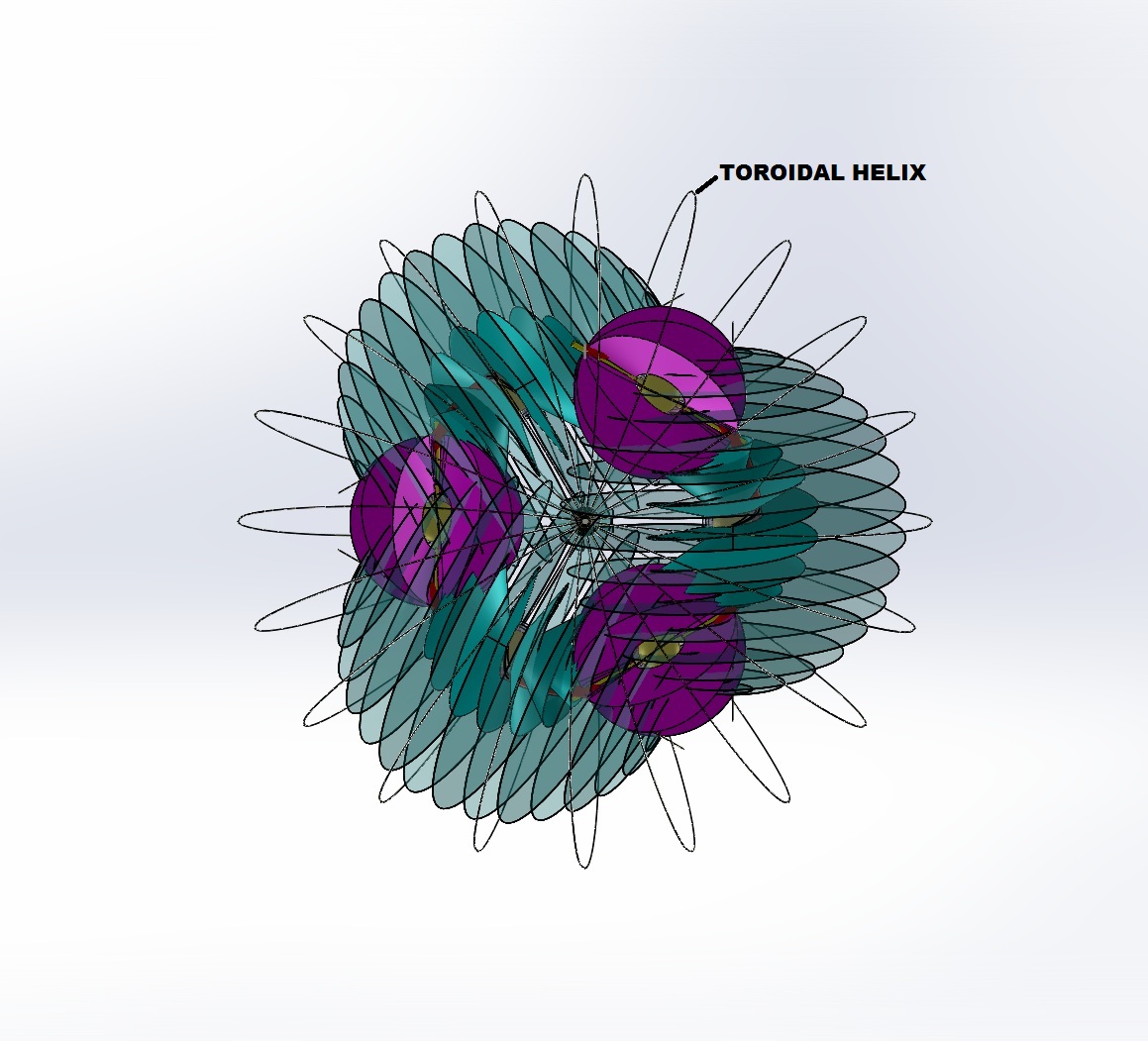
What property of this allows the concentrated vectors to act upon another object, such as the iron rod in the solenoid? Conversely, what allows a magnet moving in the path of the central axis to generate an electrical current? To explore these questions, note the similarity of the EM field to the spirals. I maintain that the electromagnetic field is generated by the spirals and is a toroidal helicoid in form. Note that in a real coil the slope of the lines would be more vertical as they would be more tightly packed and the coil would be wound with a flatter slope. Similarly, the toroidal helicoid would also have its lines more vertical as it becomes denser. The representation shown is reduced in compaction to avoid obscuring the rest of the model. That gives the field lines a greater slant.
Nothing in our definition of the veil allows it to do work though. For that I must generate another axiom to those proposed in Intermediate UU:
AXIOM 6 Veils of multiple licosoids may combine to exert force when compacted together in sufficient concentration.
This is the condition in the center axis of the solenoid. Due to the direction of the electric current's flow and the winding of the spirals, a polarity is created along the axis. That polarity is transferred to the electrons of the iron rod in the center, magnetizing it. There are several forces acting to restrict current flowing through a coil. Some of the veils of the S∞ will be restrained by resistance of the wire, back emf, etc.. It is these that reform into the toroidal helicoid and constitute the magnetic field of the solenoid. They are not destroyed and follow a path which concentrates them in the center. It is this intense concentration of overlapping veils which combines to create a magnetic field. In the article "Atom" it was posited that a veil which had been wound to S∞ would achieve such a density at the center that it would transition into a different kind of object. That was used to illustrate the difference between a proton and an electron. Here the compaction and uniformity of alignment of veils is given the property to force the adjoining veils of the electrons of a ferromagnetic core into compliance. That compliance drives a complementary magnetic field in the core.
Conversely, a magnetic rod will generate a current flow when encountering the concentrated veils at the center of the coil.
Addendum 10/24/2013
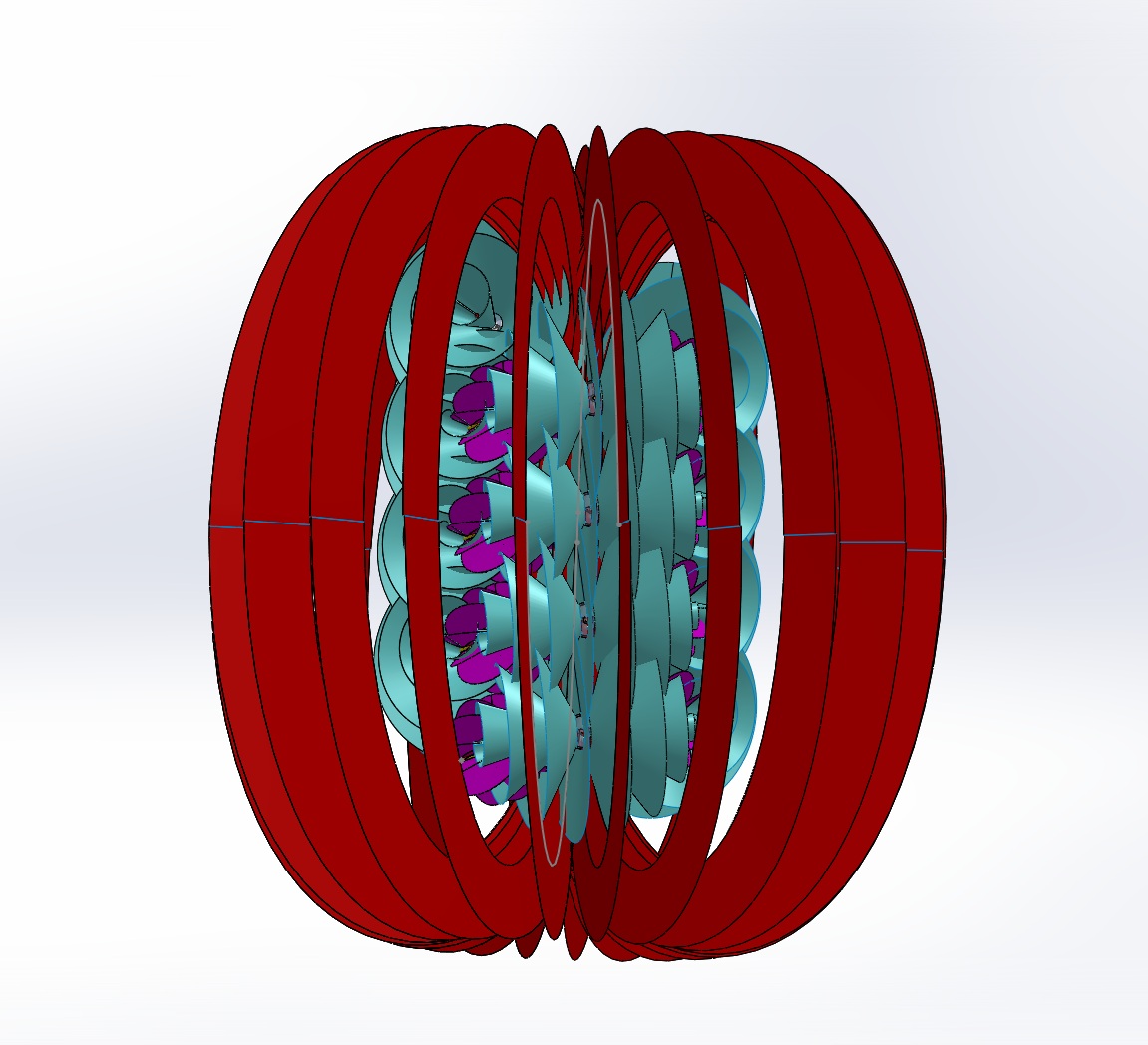
Here are two more images showing the alignment between the spirals and the electromagnetic field. Unlike the illustrations above, the chirality or handedness of the spirals was changed to better illustrate the fit. Each spiral climbs up its vertical axis clockwise. The others are counterclockwise. Also, the toroidal helix has been changed to a helicoid-as well as my cad system can render the math.

Text and Images Copyright 2013, Mike Mongan, Oak Park MI
RETURN TO:
M2 Solids Homepage
Science and Math Homepage