In "Basic Unit of the Universe" I wrote, "… we cannot posses a concept of the nature of reality that transcends our geometrical understanding". (Links are given at the end of this article.) Throughout these writings I have been proposing a new geometry. Now let us see what this geometry has to say about good old fashioned force. What happens when you use force to push something, say a pebble, with your finger? Most of the definitions I have seen don’t really help, "an influence on…", "a quantity that..", and so forth. Science books usually go straight to F = MA, which is how it can be measured.
The simplest response is that the atoms in the part that pushes, shove the atoms in the part that get pushed. Space however is not made up of matter alone. Doesn’t all the matter stuff compress until solid parts are all pushing on solid parts? No, the space is still there between the elements of matter. The older views of classic subatomic particles being the simplest elements no longer appears to be complete. Some theories have proposed quarks and another, strings as being the simplest. We consider the saddlemniscus, saddlem for short, to model the most basic element. Thus far in this series we have only examined one to see its nature. The process of energy gain and loss is what we will investigate here. In this article we will examine the interaction between two and see if we gain insight into force.
The empty part of space, the place where there is no matter, is what I have called the veil. In "Intermediate Unit of the Universe", I described a saddlemniscus as being composed of two parts, a nexus and a veil. The veil is a two dimensional sheet which is twisted until its 2d-ness becomes 3d-ness in the nexus. The way in which the veil is twisted is described in "Basic Unit of the Universe". The way to make one from paper circles and tape is shown. It has straight line radii out from the nexus in all directions. They can be either left or right handed. Each radius is an infinitely long, straight line. We allow the veil to have mass but no thickness.
The veil is space filling. In other words, there is enough of it to cover all points on any sphere of any radius. We also said that the veil does not move, the nexus moves about within its veil.
In "Density" we demonstrate that the saddlem has a density gradient, which results in an infinitely dense point center. To the veil, the nexus is a point in its two dimensional world. The nexus also exists in the three dimensional world as a physical object. In this system, it is considered to be the basic unit of matter. So there we have different viewpoints of the same thing.
The formula developed in the article on "Density" approached infinity as a limit. When you approach something as a limit you never actually get there. The infinitely dense center is implied.
We established that each nexus connects to every other nexus in a straight line manner at any instant. After all, the radii of saddlem are straight lines. As two nexii move with respect to each other, their common lines change. Each has radii that point in all directions. So as the one pair of radii disconnect, there will always be another pair of radii connecting. I will use the term "rail" to designate the common part between collinear radii of two saddlem. I will designate the two saddlem as * and # (less confusing than a and b, don’t you think). You can think of the rail as an entity connecting two nexii as they move, lengthening or shortening, changing direction, as the case may be. Just remember that in reality the components are constantly changing. The rail is only a convenient construct.

As these radii are infinite in extent and there is a universe full of them, there will be many rails collocating. Think of * and # on an infinite straight line at an instant in time. The rail lies between them. But on either side, the radii continue outwards. There can be other nexii that lie on the same straight line. Taking the line from one end of the universe to another, that can be quite a lot. Each also has a rail with every other nexus on their common lines. Quite a web. The stars do not shine for us alone. They shine in all directions. So with this.
In "Intermediate Unit of the Universe", I showed how the veil can have different configurations. We called those the spiral, whorl and ruff phases and gave equations. We also related the phases to increasing energy stored in the veil. This did not require additional veil to be added. All three forms are space filling, so there is no room for additional 2d material to go. We already have all the radii the system can take. How then does it store energy?
Say that the distance, however small, between two adjacent radii is b. How can there be distance between adjacent radii, you ask? After all, they are side by side. Yes, but they are radiating from a common point, the nexus. This problem is common to the idea of radii. It applies to every circle. Radii spread apart as one gets farther from the origin. What lies between them? More radii. But we started with two adjacent ones, where did the others come from? A plane is sometimes described as complex- composed of both real and imaginary numbers. The imaginary number is usually denoted as i and is equal to the square root of negative 1. On such a plane, a point can be denoted by x+iy. A line can be composed of such points. Importantly for this argument, the space between lines, in this case adjacent radii, we consider as imaginary area, i².
The distance spanned by three in line would be twice b. As the system changes configuration, curvature is introduced. The distance between the two points now becomes b + i. Since every point has been covered, new material cannot be added. All I can do is to add imaginary area, i ².

The veil is complex, having real and imaginary components just as the complex plane. I contend that energy is stored in this imaginary area. When the configuration is changing to increase curvature, the veil is drawing in energy. When it is decreasing curvature, it is dispensing energy .
Which phase can hold the greatest potential energy? The spiral is longitudinally oriented. It only changes directions in the simple "s" at the poles. It does spiral upwards and that varies from flat and so can store some potential. The whorl phase can be consider as the addition of a sine wave on top of that spiral. Since again, we have all the veil we can handle, this reduces the amount of spiraling and increases the amount of whorling. At some point the wave has absorbed all the spiraling and achieves the ruff phase. The ruff is latitudinal, it changes direction every 180 degrees as it turns at the poles. But, its surface is relatively flat between the poles. Which would have the greatest curvature, hence the maximum i ²? The whorl would. There the system reaches its maximum amount of chaos. So it would be able to store the greatest potential energy. Think of it as though it were a tiny capacitor with a spiral phase on one side and a ruff phase on the other.
In "Basic Unit of the Universe" we showed how to construct a saddlem out of paper circles and cellophane tape. If you have never made one, I suggest you do so. They are fairly simple to make. Construct one of 5 or more circles and see these phases for yourself.


This whorl phase then is the source which can discharge via one of the other two phases. In the ruff phase, a pole is created by the aggregation of all the radii together. In the spiral phase the distribution is rather uniform. This suggests that when the ruff phase is the conduit for energy discharge, it would be primarily in a linear manner. The spiral phase would discharge in a spherical manner. The rail is the mechanism by which both would happen.
The only thing connecting * and # is the rail. Look at it from #’s point of view. All it knows of * is via this rail. That sums up their interaction. If it perceives an energy event from *, it does so in a one dimensional manner. That is certainly compatible with force, which also acts in a one dimensional manner. From *’s point of view, a rail can be described as a vector - length and direction.
The rail has no density gradient, it is composed of two radii. Nor does it perceive a wave in the classical sense moving down its length. It stays straight and its density does not change. There is no AM or FM for it. How then can it "do" anything. To understand that we must delve into the nature of the rail.
Energy is being stored and released from the two dimensional veil as i ². To get anywhere it follows a rail or rails. The rail is one dimensional but has physical interpretation. It is made out of veil. The i ² converts to a one dimensional value. There is the linear manner in which this can be done. Normally when we think of squaring something it involves multiplying the sides of a rectangle and so forth. The square is related to an area. However, there is also a linear square, like the square on a number line. The geometric method is given in the Appendix. Click here to jump to it.
After you have jumped ahead and read it, return here. There are a couple of comments on the material in the appendix here. Note that the relationship can work two ways. It depends upon our choice of unit. Remember we started with a given length. We then developed the square as if the given is less than or greater than unity. It is our choice. In one case the square is longer than the original. But, if we chose the smaller relationship, the square is smaller than the original length. This is because the square of a fraction is smaller than the original, i.e. 1/2² = ¼.
It is the veil which first receives and transmits energy. The nexus is matter. Matter and energy are interchangeable but do not appear to do so in ordinary events. These veil to veil exchanges account for normal physical processes. The function of the rail is to provide a conduit by which energy in the form of imaginary area is converted to a linear equivalent and then reconverted back to imaginary area in a receiver.
So far, nothing has moved. We have simply described a mechanism by which energy can be transferred from * to #. But we have not taken into account #’s ability to receive it. That depends upon its own state. It may be at full potential and have no capacity to accept more i ². In that case, it may be forced to relocate to a position compatible with the rail. That may be farther or closer depending upon the relationship to the unit chosen. That is a simplification. It is better to say that the *# system moves to accommodate the required rail length. In practical terms, they will each be a part of larger systems. That will effect how much mass moves where. Regardless, this gives a mode by which mass may be moved while space is maintained in the interstices. For this discussion we are trying to keep the system simple, only two saddlem. At its simplest there is yet another major contributor which must be considered and that is density. We have been examining the quantity of energy to be moved. We will now examine the capacity of the rail to handle that energy.
Take another look at the density difference ratio, DDR, of the veil. This is the same ratio we developed in "Density" with a slight modification. Here is the equation for it and its graph. The variable, x, is defined as the fraction of the unit radius we are considering. We set a unit radius (radius equal to1) and some fraction of the distance from the center. The ratio of the inner portion to the outer portion is examined at that point. Y represents the ratio of the density of the inner portion to the density of the outer portion.
12/2/04 Hipnote: If you have read the article on Density, you may have noticed that the DDR equation is different. The variable there is n and it is equal to 1/x. N as we mentioned is the denominator of a fraction. X is the fraction directly. Also the ratio has been inverted here to show the inner over the outer. Hope this didn't cause confusion.
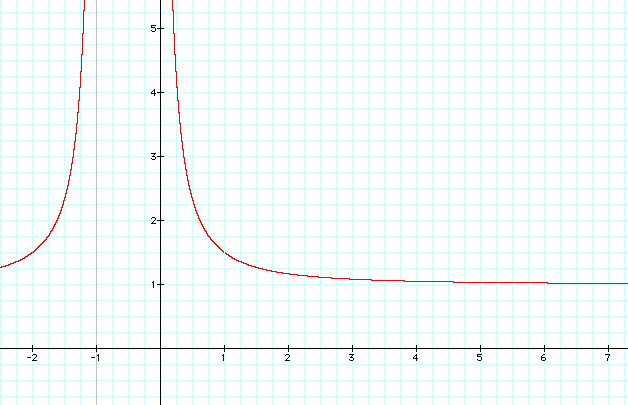
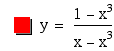
Figure 4. Rail Connecting Nexii
At x = zero, y is infinite and we are at the nexus. When x is equal to 1 we are examining the unit radius itself- whatever that radius was chosen to be. The value of y there is nan, not a number. For values of x to the right of that, we are considering the reaches beyond the unit radius. When x reaches infinity in the distant reaches of space, the ratio is virtually 1:1. There is no density difference at the outer edge of the universe. We will not consider values of negative x at this time.
The number of degrees of our saddlem does not influence this. The above is as true for one circle in a globe as it is for many. The saddlem has been specified to be composed of an infinite number of circles to represent physical space. We infer that, at the center, a 2d veil will transition into 3d space.
What of the rail between * and #. For argument, I propose that the capacity of the rail to transmit energy, Rc, is equal to the square of the DDR divided by the physical distance between them. (This assumes that both saddlem have equal DDRs. )
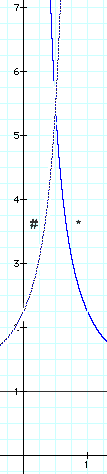
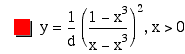
Figure 5. Between Two Nexii
It is based upon the combined curves of the two saddlem. Since their radii would be pointing in opposite directions, the graph of # in figure 6 has been mirrored to the left. Its y axis is at x = 1 and its positive values are to the left. The point where they cross, Rc, is half the distance between them. They each contribute the value of the DDR at this location. Think of it as a virtual cross section. The graph has another interpretation.
The veil is like a soup that gets thicker and thicker as you approach the center. Let’s examine the soup of the veil adjacent to the nexus. If it gets soupier it transitions into nexus. How much soupier? That depends upon how close to the point where x = 0. Call the point next to it, 1/(¥ -1). We are looking at two nexii, they would each have this soupiness. They would each have this point next to the nexus. ( I refuse to call it the nextest point.) At some closeness, *’s 1/(¥ -1). overlaps #’s 1/(¥ -1). This is their minimum distance.
The physical separation between two nexii at any instant is d. This distance can be anything from the tiny, minimum distance to light years apart. If they are at or very near the minimum distance, the curve between 0 and 1 is compressed into that area. As the distance between them increases, the relative distance between 0 and 1 stretches and the curve fits to that. As we stretch out the curves, the value of Rc drops. It would also be multiplied by the inverse of the distance between them, 1/d.
In figures 6 and 7 only *'s contribution is shown. The crossing point with # is the y value when x = 1/2. There will be some separation between * and # at which the odds are equal that they will lock together or repel each other. This we call the "neutral distance" and assign it the value of x = 1. The value of d gives the physical separation with respect to this neutral distance.
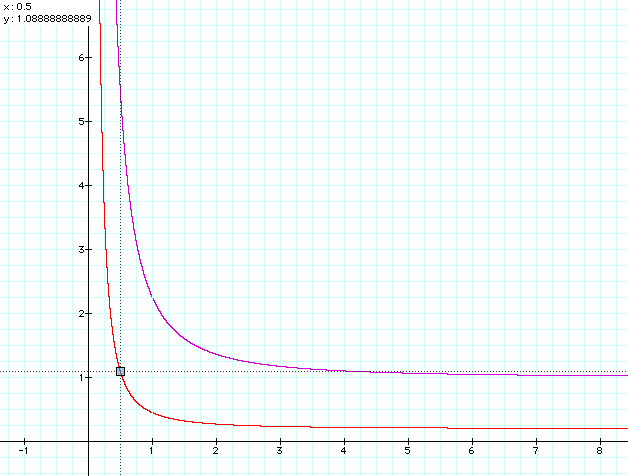
d=1 in magenta (ref.)
I postulate that in the area of the rail, the veils from the two can add enough to each other to transcend the 2d boundary again. Only this time it is into the first dimension. Let me say it another way. A connectedness is created which can result in * influencing the state of #. The soup of * is thick enough that adding the soup of # gives the rail a capacity. That is indicated by the point where the two curves cross.
The physical distance between the * and # determines soupiness. In i ² is the potential available and in Rc is the capacity to handle it. In general, when two nexii are close the rail has the capacity to move large amounts of energy. This diminishes rapidly within four or five times the neutral distance. From a few times the neutral distance out to very far apart, the rail has little capacity to carry energy.
Any two saddlem will have a common soupiness between them. It may be thick or thin dependent upon their closeness. Their relative motion will be approaching or separating in any encounter. They will often be part of larger systems in atoms, molecules, stars. That will make our simple explanation more difficult. As we discussed before, the donating veil may be in either the spiral or ruff phases. It may be dispersing energy in a spherical or a linear manner. It may be wound dextro or levo. That will all effect how much energy * is being directed at a particular companion # and how it receives that energy. So, a spherical event a light year away will be minimal. Compare to an electron giving off a photon. That photon effects every other object in the spherical area centered about it, even along a rail to retina cell in an eye looking in a far distant telescope in another galaxy. A linear event within the confines of an atom can be a much more powerful discharge.
Eventually the energy that * sends to # will arrive there and the system will find a new equilibrium. Sometimes they go on their merry way. Other times they remain locked in a pair. What is the nature of this binding which is able to keep them together even when they are of the same charge? The normal forces of repulsion are overcome by what has been called the strong nuclear force. When two saddlem get closer than the neutral distance, d has a fractional value.
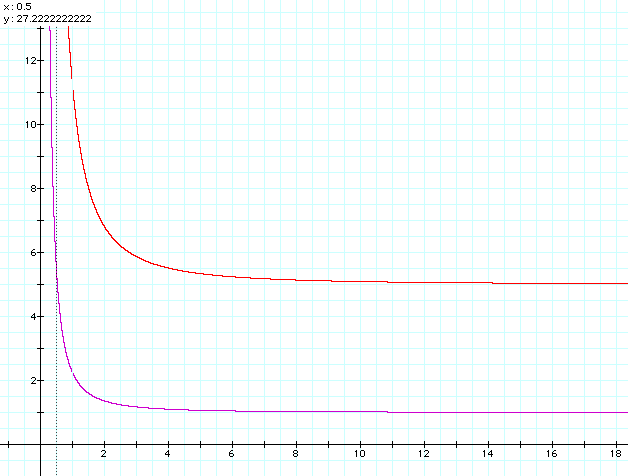
d=1 in magenta (ref.)
As with the choice of a given length smaller than the unit in the Appendix, this indicates a contraction of the rail. It would give rise to a very powerful value for Rc.
There is another aspect to the rail that occurs on the other sides of the *# pair. Up to 3 or so times the unit value, the potential of the rail is still significant. After that it dwindles rapidly. The radius from * continues on through # into this far side area. There will also be a radius from # in the same location. They comprise a second, the far side rail. Its action follows the other option in our linear squaring. Distances above the unit would square to larger values. The effect of the far side rail would be to expand the system. Far side rails will occur in pairs on either side of *#. The overall effect of all these rails would depend upon the distance separating the two saddlem and their respective charges.
If the receiving saddlem cannot accept the energy it can retransmit it to other saddlem via the rail it shares with them and so forth. This would be the case with electrical current. There are of course special conditions required under which this would be possible. Excess energy can also appear as heat.
Lastly, there are high speed collisions. This is what you see in the photographs of cloud chambers. Mass cannot move fast enough to prevent a violation of the minimum distance rule. There would be no room for a rail for them to interact in the normal manner.In this case the nexii split into a combination event so that the matter -energy going in equals the matter- energy coming out. The system is conserved so that nothing disappears and equilibrium is eventually reestablished.
All of this is occurring in a temporal universe. To describe force, I must accommodate time. We must resolve the difficulty of action at a distance vs. time. In other words, why does not all this happen instantaneously? If a photon is emitted at a distance from us it takes time to reach us. Yet, if the rail is simply squaring, why is it not instantaneous? Did you note that in the DDR, the value of y was undetermined when x = 1? That implies this point is instantaneous. But it is also the unit point. The unit begins at the nexus- veil boundary. It is sequential outward from there at the start of an event. It moves outward until it finds its resolution in some #. When it does, that becomes the unit for the arena of the moment. I believe this process is the root of the speed of light.
Navigator to the entire website located at bottom *************************************************************************************
APPENDIX to FORCE
by Mike Mongan
September 24, 2004
There is a geometric way in which a line can be squared and produce a linear result. This is different than marking a number on the number line and then marking its value squared. Remember in the Dimension series I showed you my notation for the chords of a polygon. The shortest chord of any polygon is denoted as A, the next longest as B and so forth until you reach the diameter, the longest possible chord. I use the cent Ë sign to designate "chord". Last is the number of sides of the particular polygon you are dealing with. In the example below, AË 10 denotes the first chord of a regular decagon. I will only consider regular polygons with an even number of sides in this article. My investigations into geometry produced the following relationships for the decagon. They seem to be true in general but that is a digression.
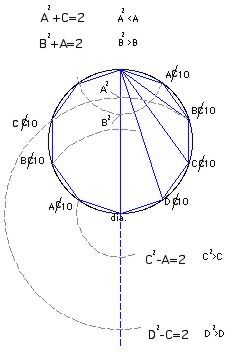
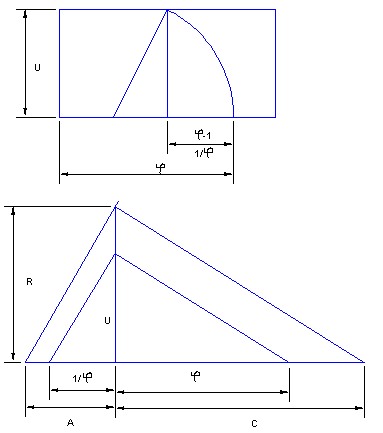
As the figure shows, there are a number of ways in which a line may be squared. The circle has a radius of one. The chords of a regular decagon all have lengths which are based upon the golden section, denoted by the Greek letter phi,j. It is easy enough to construct a right triangle with the appropriate ratios. Then any length may be related by using proportional triangles.
First, create a golden section with respect to U, an arbitrary length.
If a decagon is inscribed within a unit circle, then AË
10 = 1/j. Note that 1/j is also equal to j-1. CË
10 = j. The radius of the unit circle, R, is equal to 1. Diameter is 2.
Take the given length to be A, the first chord.
Or take the given length to be C, the third chord.
Mark off A or C as shown. Use proportional triangles to find R, the radius of the unit circle.
Square lengths can then be determined by the rules given.
A² = 2-C; A² < A
B² = 2-A; B² > B
C² = 2+A; C² > C
D² = 2+C; D² > D
In general this summarizes what I believe is a general rule for any –ogon with an even number of sides:
As we have shown above, knowing the lengths allows you to determine the square. The decagon was chosen because all of the nifty relationships among the chords are in terms of the golden section. If you look at regular polygons with higher numbers of sides, AË N gets smaller and the 3rd longest gets longer with respect to a unit radius. In the hexagon the first chord is the 3rd longest so they converge, but the rule still holds. There are many other relationships, but that is a discussion for another time.
RETURN TO Force:Discharge, How The Rail Transmits Energy- where you left off
*************************************************************************************
All images and text copyright 2004 J.M. Mongan, Oak Park, MI