Up until the late 1800's science in general accepted the existence of the ether, an invisible medium that was believed to permeate space. After the experiments of Michelson and Morley in 1887, that belief turned to doubt. Their results were eventually taken to disprove the existence of the ether altogether. Nowadays we read of the probability that the universe is filled with cold dark matter. This stuff is needed to make up for missing mass, etc. Sounds like the same load to me. What I have been proposing is an alternative that may be of assistance. I don't say this is true, because I don't believe that us wee folk can really root out the exact truth. We can only make approximations that may be more or less effective in dealing with our world. I believe that Drs. Michelson and Morley did not find evidence of the ether because they were looking in the wrong dimension.
This article is a study of the Unit of the Universe on an intermediate level. The Unit of the Universe is my proposed model of what makes matter and energy tick. We will propose definitions and axioms. Equations of form will be given. An explanation of quanta, time and space will then be derived. If you have not read UU Basics, I suggest you do so. Illustrated instructions are given on how to model it using only paper and tape. This material is not a part of the Standard Model of particle physics that is generally accepted by the scientific community. With notable exceptions for gluon and gravitons, I do not believe that my UU Model conflicts with the Standard Model. I believe it compliments it and gives a method by which the known physics can happen. For an excellent, quick and easy review of the Standard Model click The Particle Adventure. This site is by the Particle Data Group of the Lawrence Berkeley National Laboratory and has many materials for teachers and students.
DEFINITIONS:
1. VEIL An infinite two dimensional sheet having area and mass but not volume. I have chosen the term veil to distinguish this from the purely geometric construct, plane.
2. NEXUS The smallest entity that has material existence in our world. It is the result of the twisting of a veil by an infinite straight line generator about a point center. When the twisting of a veil has achieved the upper limit of the density gradient, a nexus is formed. Nexus in Latin implies joining. In the Unit of Universe system, the nexus joins the worlds of matter and energy. I will use "nexii"; for the plural as we say radii for the plural of radius. It isn't quite proper Latin but it sounds better to me than nexus or nexuses.
3. SADDLEMNISCUS (saddlem for short) The combination of a veil and a nexus. An infinite saddlemniscus occurs when that process has been continued until all points on a concentric sphere are penetrated by some radius of the saddlem. What we register on our side of the universe as a basic unit of matter is, from a two dimensional point of view, the center of some saddlemniscus. The term "center" is used loosely, as we will see.
AXIOM 1
No two saddlem may share the same nexus.
COROLLARY
A single nexus may only host a primary veil and its dual.
Discussion:
How many points can surround a point? In geometry, it is an infinite number. Many nexii may be adjacent. But each nexus must be unique. Note however the phenomenon pointed out in Dimension Part 4. We consider a saddlem to be generated by a line rotating about a point. Its two ends are separately generating the primary and its dual, like a positive and a negative. Several of the equations below consider only the half generated by one radii as opposed to a diameter. The reason is to show the concepts in a simpler context. Take a look at the generation of a cone by a line to start.
Take a look at the generation of a cone by a line to start.
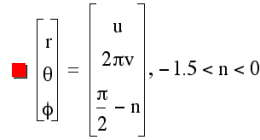
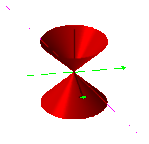
Fig. 1 LINE, CONE AND CIRCLE
(Hold mouse over picture for animation.)
Note: These are parametric equations in spherical coordinates. If you are not familiar with them, don't worry. there's nothing tricky here. The graphs show two arrows. These point in the positive x and y directions. The positive z axis points upwards. The r term is simply the radius of the function. A range of 0 to 1 for r would be the upper cone only. The range of -1 to +1 (shown here) is the diameter and yields both cones. It generates the primary upper veil and its dual, the lower. The next term, theta, indicates the angle on the xy plane. It is centered at the origin. It is measured from the x axis moving counterclockwise around z. 2 pi indicates one complete revolution. the last term, phi, is also centered on the origin. Phi indicates the angle from the z positive axis for any particular value of theta. You can think of these as similar to how places on the Earth are measured in longitude and latitude. Theta is east and west, phi is north and south. N is the variable.
AXIOM 2
No veil can intersect itself.
Discussion:
Each veil is a unique structure. It cannot pass through itself otherwise its uniqueness would be violated. Its dual is also unique by itself. However they may intersect each other or even be coplanar.
COROLLARY
Veils of two or more saddlem may intersect any number of times.
AXIOM 3
Between any two nexii there exists a common line segment.
Discussion:
By definition, each infinite saddlem will have one radius pointing in any possible direction. So will any other also have some radius pointing back to the first. The radii will be collinear. The nexii will then share the straight line segment which lies between them.
AXIOM 4
Motion is the translation of a nexus with respect to an external framework.
Discussion:
The twistedness moves, the veil doesnot. Being infinite, it is already everywhere. To a nexus there is no condition of rest or motion. Tie a loose overhand knot in a string. Put your finger into the knot and move it along the string. The knot stays the same. (Note: A nexus is not a knot in mathematical terms.) In a similar manner, the nexus can get anywhere in the veil by translating its twistedness along some radius.
The nexus does not have an absolute position on a veil. Since the veil is infinite, it has no overall frame of reference. It only appears to move when we assign it a frame of reference. It has none of its own. What we see as motion does not mean that a point center carries its veil wherever it goes. Like the exercise in Gravity, with the two fingers from two hands, it can move about its infinite, space-filling veil unimpeded in its world. Its veil doesnot go anywhere. So if it is at rest or in motion to us, the nexus doesn't know it. To the nexus, the veil appears to be flowing through it, repositioning itself. This will not occur unless acted upon by an outside force. Sound familiar, it is Newton's first law.
So what happens when nexii collide?
Several things. Going again to the Gravity exercise, what if we were to place two sheets of plastic food wrap, one on top of the other and repeat our two finger, two hands exercise. We would not be violating any axioms. The veil is two dimensional and has no thickness. It has area but not volume. Their nexii would be separate but adjacent. If we were to impact these two with a third, it is allowable that they could dissociate, i.e. fly apart. It is also allowable that the third could associate or agglomerate. A veil may not cross itself, that preserves its uniqueness. But veils from different saddlem can cross each other. So nexii can move together or apart. They just can't collocate. The huge question is this. If veils penetrate each other, do they do so without involvement? Is there a consequence to interaction?
Let us examine the argument from Density Gradient first. We compared the volume of a sphere to the area of a circle of the same radius and considered a boundary at one half the radius. We then postulated that the plane bounded by the circle had a uniform mass. This allowed us to compare the density of the outer half with that of the inner half. We found that the inner half was more than twice as dense as the outer half. This ratio would apply no matter how many circles we added. As we have demonstrated, the saddlemniscus is considered to be the addition of circles. So we take this ratio to be true for it also. If we take half of the half and compare it in the same manner we get the same result. We could continue this process indefinitely inward or outward. So we say the saddlem has a density gradient. As we continue to halve the radius, we approach the geometric center point as a limit. We then infer that the density at the limit is infinite. What does that mean? To simply say infinite doesn't tell us anything about the state of the system. It has no relative meaning. It goes against the normal definition of density because we are talking about a sheet with no thickness. We have area but not volume.
I have also said previously that energy is a two dimensional phenomenon. This relates the veil to energy. But we have also now said that when the veil is concentrated in the manner of the saddlem, it manifests itself as matter. They are then different expressions of the same thing. That is not new, Einstein said it. What we are adding here is this:
AXIOM 5
Neither matter nor energy may exist in pure form.
One will always entrain some of the other to a greater or lesser degree. So, the veil can have mass. So also the nexus can have energy.
What about the part of the veil next to the nexus? If we have fallen through the black hole of our nexus from one dimension to another, we did not do so instantly. It came along a gradient. It would be difficult to say where nexus leaves off and not-nexus begins. Areas of the veil adjacent to the nexus exist in a soup of space where density is almost but not quite matter. That is what allows our nexus to interact with energy in complex manners and not simply behave like a billiard ball.
To see this better let us play with pipe cleaners again. Twist ties will work also but are kind of short. We are going to coil them around a pen like a spring, or helix. A helix can be dextro or levo, i.e. right or left. Here is how you do it. Hold a pen in one hand pointing sideways in front of you. Take a pipe cleaner and hold it between your thumb and the pen so that the pipe cleaner points up. Twist it around the pen going over the top. Leave a little room between the coils. To do the opposite, hold the pipe cleaner so that it points downwards. Twist it around the pen going under the bottom. How do you know if it is right or left? Put it in your palm running along the creases. Gently close your fingers. Look at the coil closest to your index finger. If the coil is pointing in the same direction as your fingers, then the coil is that hand. If not, it is the other hand. Make at least three of each hand.
Take two of the same hand and put them together, side by side. Notice how they fit. They go together and come apart without much difficulty. You can add a third one of the same hand with ease. Let us call this twin binding. This is the same form we made in the DNA demonstration exercise. Next take one left hand and one right handed coil. Try to put them together as before. They will not join in the same way. Is there a way in which they will combine? Yes, you have to screw them together. It is not that hard to do with pipe cleaners, but you have to be careful as you go along. What you end up with is an interlaced double helix. Notice how tightly bound together these are. A simple hit will not separate them. Let us call this laced binding. Now take a third helix of either hand and bring it to this laced pair. It will barely nest with its twin. But you can screw this third one in. We have demonstrated two kinds of binding, twin and laced and shown that they involve very different bond strengths.
So what has this to do with our saddlemniscus? Earlier we showed that it is really a bound helix. That was when we trimmed off the edge. We showed it is a helix with a point center. The ones you wound around your pen have a linear axis running through the center. With saddlems, it is as if the axis has been compressed to a point. So it can have different bond strengths. This occurs among particles also.
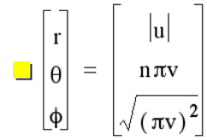
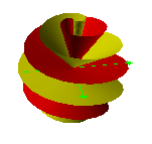
Fig. 2 THE LOW ENERGY SPIRAL STATE
(Hold mouse over picture for animation.)
This spiral phase illustrates the lowest energy state. Here r is 0 to +1 only, and phi has been allowed to seek positive and negative values. A paper saddlem of any number of degrees will follow this style of configuration to its lowest energy state. The circles of paper will spiral around the z axis. They will stack up like the parallels of latitude. But there is an excess because we have a bound helix. The excess forms into the arches through the poles. We have a whorl left over at the top and bottom. They get stretched out with one leg of the arch going one way and the other in the opposite direction. In other words it exhibits chirality or handedness. We can define its handedness like we did for our coils. Lay it in the palm of your hand with the z axis or pole pointing along the crease of your fingers. Gently curve your fingers inwards. If the whorl leads to the pole in the direction of your fingers, it is that same handed. If not, it is the opposite hand. Looking at the illustration you will see that the whorl at the north pole or z+ axis looks like a letter S lying on its side. The whorl at the opposite pole looks like a mirror image S. The illustration is right handed.
Increasing Energy
The tetrahedral saddlem shows no evidence of its helical origins. Its edge would trace a sine wave on a sphere if it were placed inside of one. Let us call this the "ruff" phase after the ruffled collars you sometimes see around the neck in Renaissance portraits. Remember that a saddlemniscus can change in both frequency and amplitude. As you increase the numbers of circles the number of the ruffs increases. If we added more circles, we would be able to form them into sine waves too. It would take more energy and not be as stable as the spiral phase.
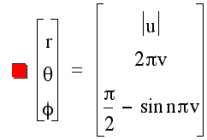
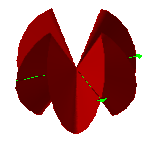
Fig. 3 INCREASING THE FREQUENCY
(Hold mouse over picture for animation.)
As we increase the amplitude, the sine waves begin forming around a polar axis. Doing this with paper circles, you will need to put in a lot of energy to keep it in that state. The form wants to fight you and seek a more relaxed state. (Don't we all.) You will also see a similarity to the meridians of longitude that are shown on globes of the earth. As the meridians cluster about the north and south poles, so do our whorls of paper. A meridian is a circle on a globe. Our saddlem meridians are not. They turn around when they reach the pole and go back the other way. At the topmost part, each whorl will have one radius next to the polar axis. As we add more circles of paper, we add more meridians, whorls and near polar radii. If we continue the process to infinity we would fill the saddlem with meridians until the entire surface was covered. We would also have compressed our whorls flat. There would be an infinite number of them clustering about the pole. But they could not all be the polar axis, that would violate Axiom 2.
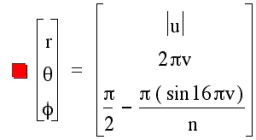

Fig. 4 INCREASING THE AMPLITUDE TO THE POLES
(Hold mouse over picture for animation.)
A famous conjecture by the French mathematician Henri Poincare about closed spaces goes something like this: If every closed loop of string on a surface can be drawn to a single point, then the space is a true three dimensional sphere. I don't know if Mssr. Poincare would approve of my solution, but it would be true of a saddlemniscus, as the string would just follow radii down to the center as it is being drawn in. Imagine a loop of string along the edge of the saddlem. If we drew it tight, it would eventually wind up at the nexus. Any loop on an infinite saddlem have some combination of radii to follow to the nexus point.
Why isn't The spiral form left handed? The reason is only because we did it that way. We could just as easily have made it the other way. In fact, if you have a paper model, you can make it other handed. It can form its own mirror image. You have to pass through the ruff stage to do it. So if we had a saddlem in its highest energy state in the ruff stage and we let it relax, it could go either right or left. I of course encourage you to saddle up some paper circles and try it yourself.
In between the ruff and spiral states is an apparent chaos of whorls going this way and that. Below is the tame version of this transitional mode.
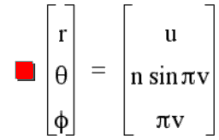

Fig. 5 TRANSITIONAL STATE
(Hold mouse over picture for animation.)
So why all this discussion of helixes and handedness. Because it allows saddlem to have a means to attach to each other. It also allows them to have different energy states. The goal of these article is to propose a geometry which provides a more natural description of our universe. In our universe, things have handedness, they stick together and come apart, they bounce off each other, they store and release energy. The saddlemniscus is my way of describing that.
Why do things appear quantified?
Look closely at the animated gif for the Ruff phase above. Notice that the fabric of the veil is not always whole. This is not a smooth and continuous function. The veil is "torn" at the x axis, both + and -. The function is only continuous for integers. For the odd integers, the function is continuous but not smooth. It terminates at the x axis only from the positive side of the z axis. It is both smooth and continuous only for even integers. They join at the x axis from both directions. I am hypothesizing that the ruff phase represents a form in which a infinite saddlem exists at higher energy. But it needs to relocate itself to different energy states. To do so in a smooth and continuous manner would require the ripping of the fabric of space, i.e. the veil. This cannot be in the normal universe. So, the system of change is restricted to the even integers. This is the root of the quanta.
SPACE
According to Axiom 3, the nexii are all connected.
The system of universe then can be considered at any instant as the totality of line segments and nexii. This does not imply that every radius will reach another nexus. Each individual saddlem is infinite and independent while connected by its commonality to all others. So the problem of action at a distance in quantum mechanics is given a method. This is true regardless of where they are located. This connectedness is a one dimensional component. The one dimensionalness has been there from the beginning. Remember that the lower limit of the licosas system is a line. That is what we approached as a limit when we slid our cone together. We have considered the nexus to be a penetration of a two dimensional object into a three dimensional space. In many respects the veil can be considered the penetration of a one dimensional object into a two dimensional space. Similarly our initial line can be considered a penetration of a zero dimensional object into a one dimensional space.
TIME
Nothing is static. All is in motion. So these line segments, the connectors, are in constant flux. Each time nexus A moves with relation to nexus B, new connectors will be established between them by others of their radii. If the segments from points A & B are noted over a time interval, they will describe some curve. I propose that time is any curve which accommodates the connectors as tangents to itself. The curve is defined by the connectors. As we complicate the problem by adding more points, all of their time lines combine to create a TIME FIELD. Like the sea, it is ever changing. Yet every particle is an extension of where it was. The totality of straight line connectors between all nexii is the instantaneous NOW. So, is space curved or straight? The answer is yes. It is linear when viewed as an instant but curved when viewed over time. Since an instant is so fleeting, eternally out of reach, we experience and remember a curvilinear space.
*************************************************************************************
All images are generated by equations using Pacific Tech's Graphing Calculator.