ADDENDUM
New equations and animations have been added. Spiral and ruff versions of the cone have been developed, the coneoids. That is found in the lower portion of this article.
November 22, 2013
The LICOSAS
This article illustrates the geometry of the LICOSAS with animations. The animations show how the different forms are related as they grow from line to sphere. It is hoped that this will clarify the series and save the reader from jumping around to different articles on the website. LICOSAS is my acronym for a geometric sequence that runs Line, Cone, (circle) SAddle, Sphere. Saddle is short for saddled lemniscate meniscus. A saddle adds degrees to a circle by tacking on more circles. As more and more circles are added, the form becomes more like a sphere. When an infinite number of degrees have been added we cover all points on a sphere. The saddlemniscus is designated as "S∞".
In spite of its mathematical underpinnings, it is easy to understand. You can model it with paper circles, adhesive tape and imagination. Basic Unit of the Universe, UU Basics ,shows you how with step by step illustrations.
The saddle has two paths that it can follow to sphere. The SPIRAL path:
The Spiral Path
Click picture for movie.
Click "BACK" to return
The Ruff Path
Click picture for movie.
Click "BACK" to return
The Spiral-Ruff Transition
Click picture for movie.
Click "BACK" to return
This animation shows how one transmogrifies into the other.
The formulae for these are given below. These are parametric equations in r (radius), theta (angle of revolution about the vertical z axis) and phi (the angle a function takes from the vertical). The program is Pacific Tech Graphing Calculator. Note that the spiral can wind either clockwise or counterclockwise.
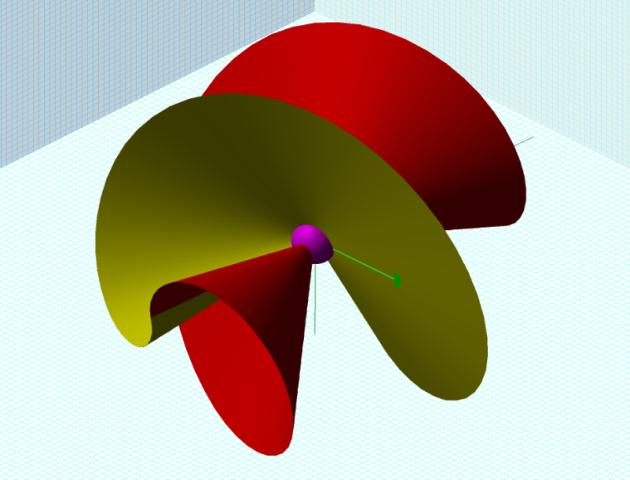
Note that the spiral form exhibits chirality or handedness. I define clockwise rotation as the saddle climbing clockwise up the z axis. If you are holding a model in your hand, point the axis up. Trace the edge upwards with your finger, it will move clockwise around the axis.

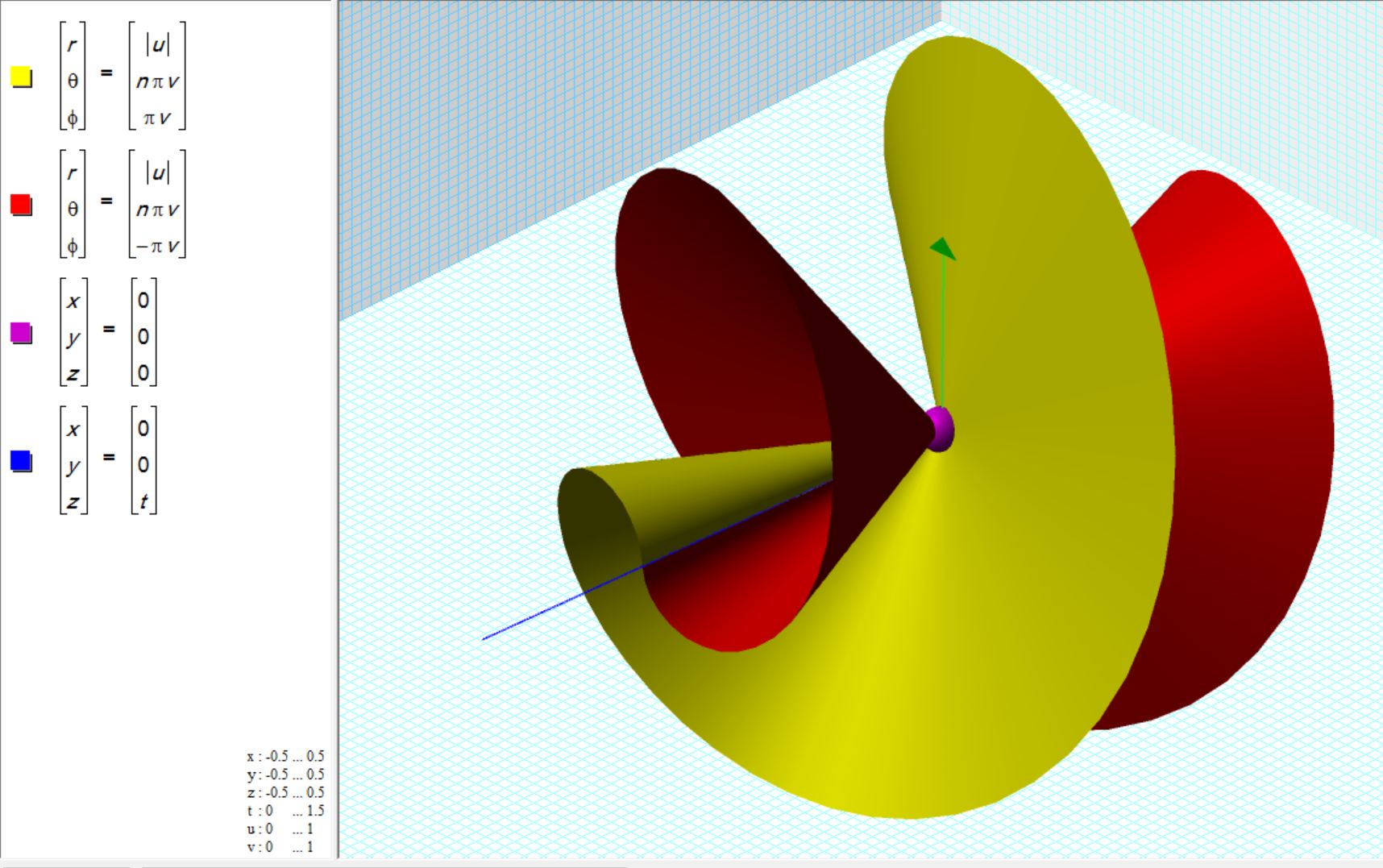
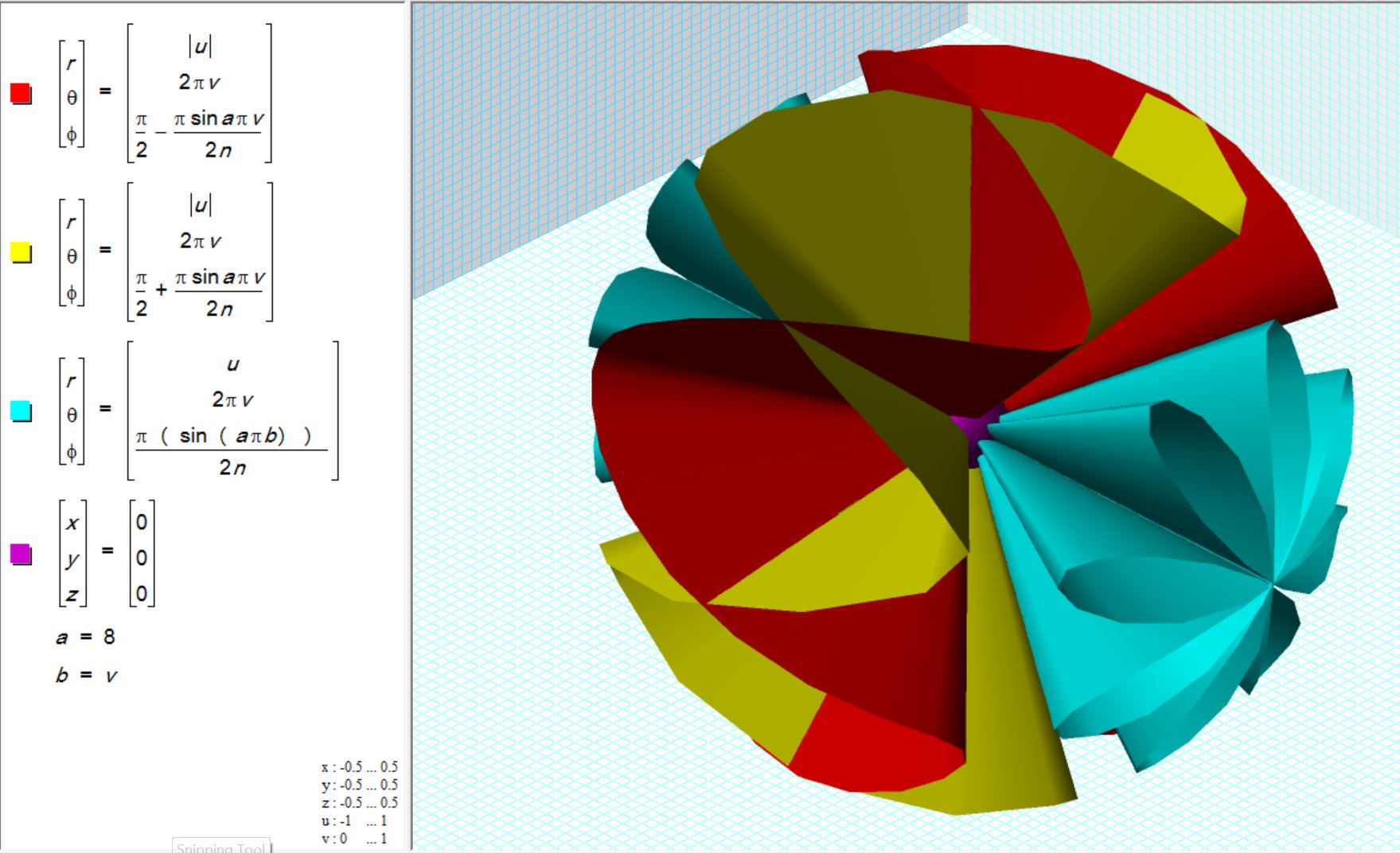
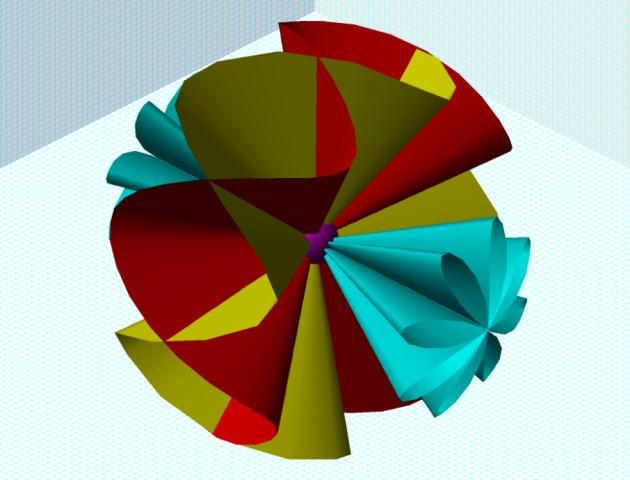
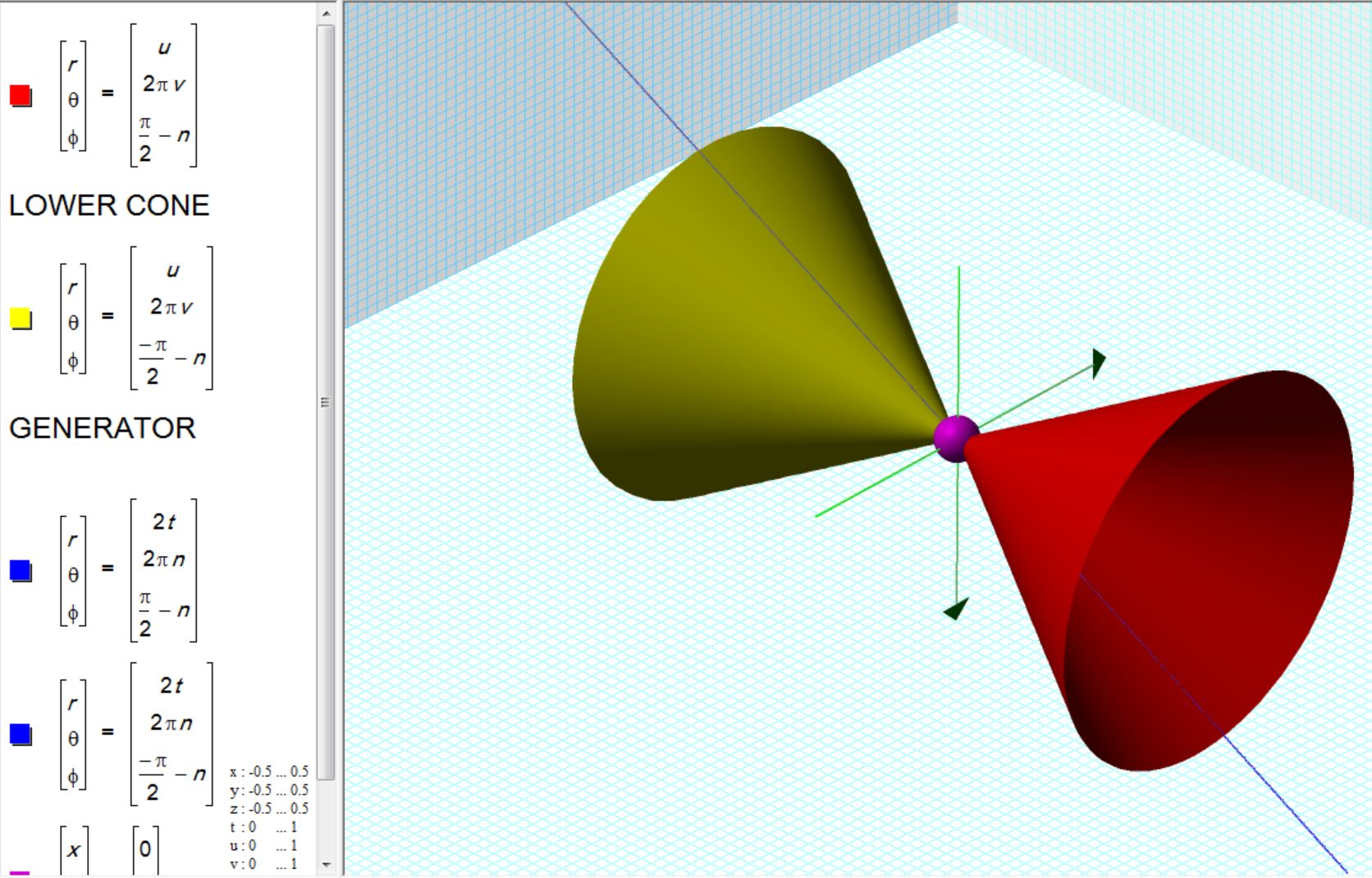
I have often felt that my understanding of the line-cone part of the sequence was missing something. The cone was just an empty vessel. An equation changed all that. Figure 4 above shows a ruff cone. This will explore that further. I call this form a coneoid. Here are the formulae with the mating cone.
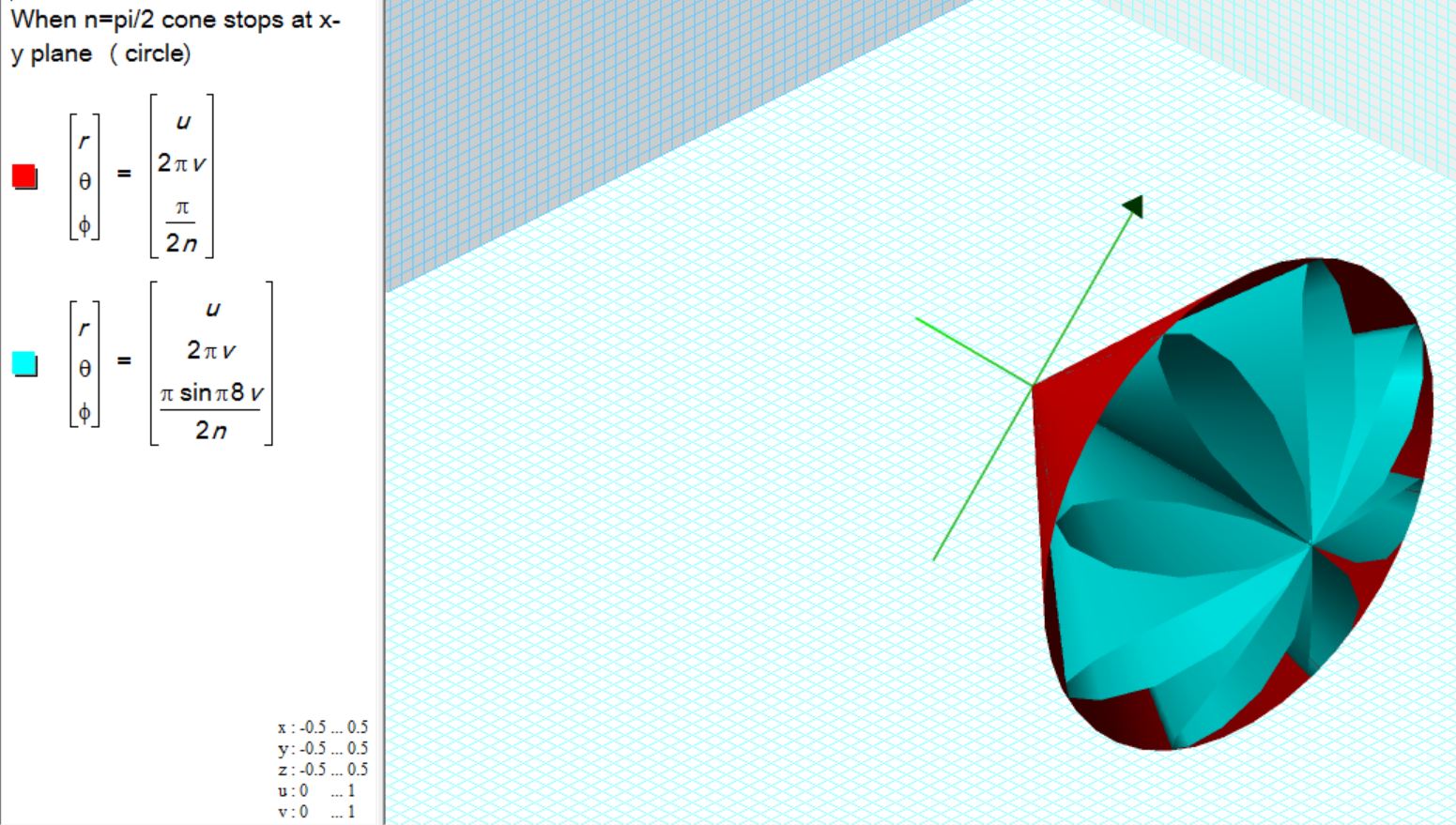
Note that the formula for the ruff coneoid transitions into the ruff saddle simply by adding pi/2 to the statement for phi. This changes its orientation 90 degrees from the pole to the equator.
The number 8 in the statement for phi is the frequency, count the 8 loops. As it approaches infinity, the cone fills. It is rounded because spherical coordinates are used. The radius, similarly, extends outward without limit.
There is a corresponding coneoid for the spiral form also. The formulae are again, very similar.
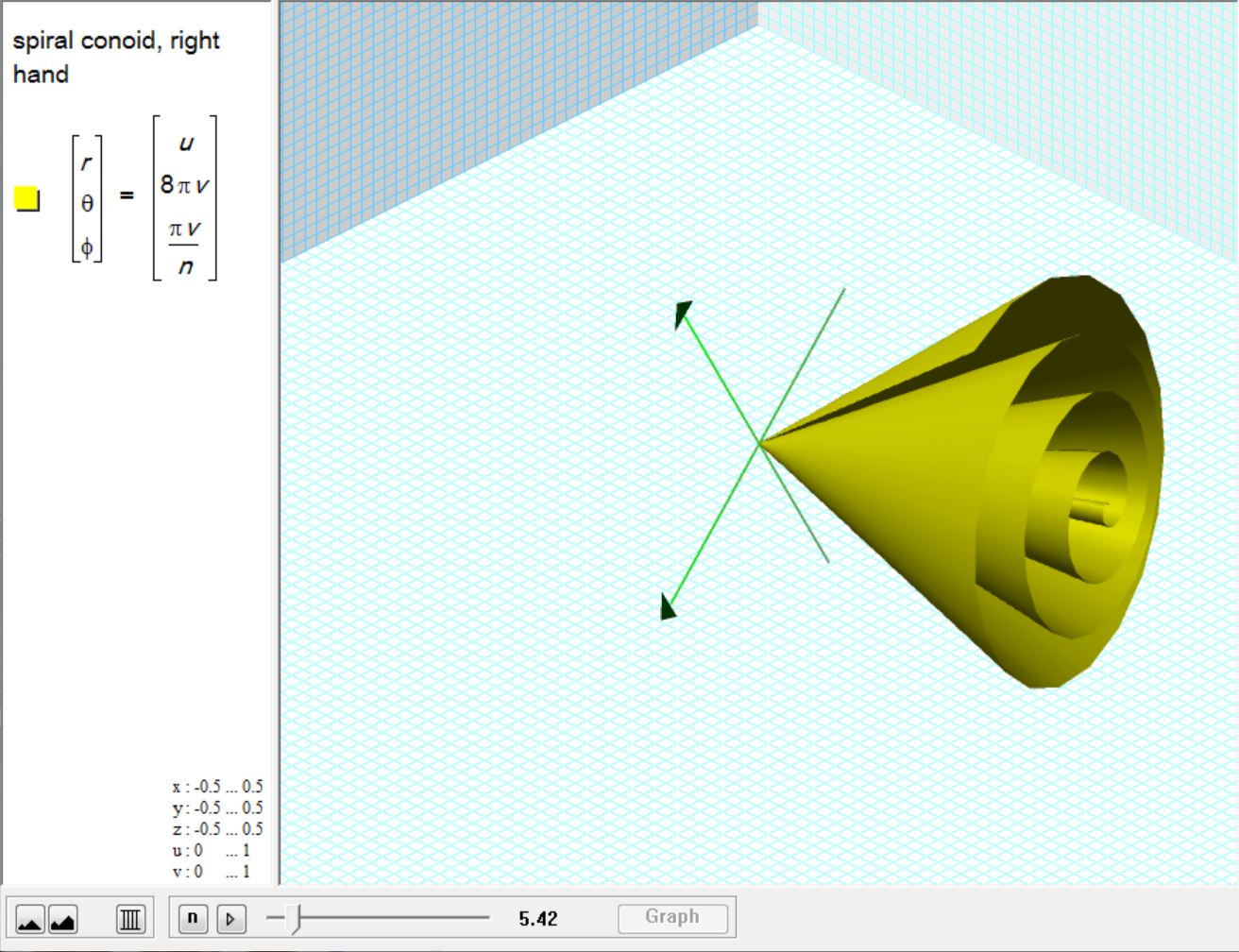
The Ruff Coneoid animated.
The Ruff Path
Click picture for movie.
Click "BACK" to return
The Spiral Coneoid
Click picture for movie.
Click "BACK" to return
Discussion:
It bears repeating here that we are dealing with the veils as defined in Intermediate Unit of the Universe . Veils are two dimensional sheets having area and miniscule mass but not volume. They twist into point centered helixes. As you can see in the animations, they do not join their edges in the coneoid form. That happens when they become a saddlemniscus, saddle for short.
As such, how many veils could be stacked on top of each other? They are two dimensional after all and have no thickness. I point this out because now we are showing that they spawn out of a line which in turn spews out of a point. What is the point?
Text and Images Copyright 2013 & 2014, Mike Mongan, Oak Park MI
RETURN TO:
M2 Solids Homepage
Science and Math Homepage
Electricity, Electromagnetism and the Licosas