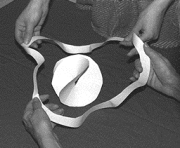
Lift up an edge from one side of the radius and place it over the top of the other edge. It makes no difference if you place left over right or vice versa. Notice that as you do this the center starts to rise up, forming a low cone.
Now slide the top edge farther in the same direction.
Notice how the cone becomes steeper as the edges slide apart. Call this action "coning", it will define the motion which makes the cone steeper. If you tape the cone together, the process of coning becomes fixed. You have stopped it with the tape. If you were to slice through the cone you would create one of four special curves called a conic section.
Because you can start by placing either edge on top, this process demonstrates handedness or chirality, coning can be left handed or right handed.

FIGURE 1 CONING
At any point in coning, you can find how much of the original circle you have used. Simply mark the position of the edge with a pen or pencil. Open it back up and draw the radius from that mark to the center. See what portion of the original circle this particular cone uses. It is like cutting out a piece of pie. With the help of a protractor, you can read what that angle is.
If you were able to keep sliding these edges farther and farther in the coning direction the cone would get so steep that it would start to look more like a line. No matter how hard you tried, you could not cone farther than a line. So we say that the lower LIMIT of the action of coning is a line. You cannot continue to cone in that direction beyond a line. Going the other way, the cone gets flatter until it returns to the original circle. Is this the upper limit?
What if the process didn't stop there and we could continue? This is like asking what happens if we could pump up a circle to over 360 degrees. Well, we can stuff an extra piece of pie into our circle. Here is how. Take the circle with the radius cut that we used to make a cone. This time we will add another circle to it. Here is the secret.
Put another circle on top of the first one. Keep the center directly over the center of the bottom one. Keep the cut radius directly over the cut radius of the bottom one.
Have your partner lift up one side of the cut radius from the top circle. It could be right or left, but let's say the right side like in the photo. Now take a piece of tape about the same length as the radius and tape it as shown. You will be taping the left side of the upper circle to the right side of the lower one. If your partner holds it in the air, you will see how the outer edge or perimeter of the circle now forms a spiral. This is like the form of a spring or a screw thread. It could be left or right handed like the cone, depending on how you taped it.

You now have two free edges, the right side of the top circle and the left side of the lower one. Take these two edges and slide them together in the coning direction. You see that you are making a cone just as we did before.
Now un-cone it, letting it go back to the way we started. The direction it takes is opposite to coning. This direction is called "saddling". Here's why it is called that. After it has relaxed back to the circle stack, continue to keep it going in the saddling direction. Above 360 degrees it takes on a saddle like form. This form can be described in degrees just like the cone. We could mark it anywhere along the process and measure it like we did the cone. It will be 360 degrees plus something more. A circle and a half would be a 540 degree saddlemniscus or saddlem for short. (See the explanation for this term at the end.)

Keep going in this direction until you can go no farther. The two free edges will butt up against each other. Have your partner put a piece of tape across them, this fixes the process of saddling. The whole figure is now united in to a 720 degree saddlem.

You have now demonstrated a sequence which runs line, cone, saddle and have seen how they are related. The circle has become a special case in the sequence between the cone and saddle. This could be compared to the number one being a special case on the number line - between the fractions and the whole numbers.
Let's see what happens as we continue the saddling process. This time we are going to make a 3 circle stack. Set one circle on top of the other circle so that the radii match, one exactly above the other, just like before.
Lift up the right or left side of the cut radius on the top circle. Tape the other edge of it to the circle below. (Hint: If you put tape on both sides of the paper, it looks smoother. Just flip the whole thing over and do the same thing on the other side of the same edge.)
Put a third circle on top of these two and repeat the process. Be sure to lift and tape the same side (right or left). Check it by holding it by its free top side, you should see the outer edge spiral smoothly from top to bottom, like a spring. It is possible to reverse the handedness here and we want to avoid that for now.
Slide it in the direction of coning and saddling to get the feel of it. Notice that the actions of coning and saddling work the same way as before. Now saddle it all up. Go carefully, you are working with paper. Take the top free edge and the circle just below it. Start sliding it in the direction of saddling. It is building up compression at the center and tension along the outside, so work gently. Eventually you will slide this free edge far enough to reach the other free edge on the bottom of the stack. When the two radius edges come together, set them together, side by side and tape them. This is a 1080 degree saddle.

There is no particular significance to the number of circles you used. More could be added. The only limit is the physical nature of the paper. It gets tougher to handle as you add more. Personally, I've never gotten above twelve. But if we had a perfect paper we could continue this process to infinity. In theory it has no end, there could be an infinite saddlem. Look at the 1080 saddle you made. It has taken a more ball like shape than the first saddle you made. Imagine what it would be like if more circles had been added. If an infinite number had been added, you would have a sphere. For all practical purposes the surface would be solid. That is the upper limit of our process - the sphere. So then our series runs line, cone, saddlem, sphere and so is called the "licosas".
But there is a big difference between this and other globes. That difference is density. If you take a block of wood, put it on a lathe and cut it into a globe it will be the same everywhere inside. A cubic inch of wood will weigh the same whether it is from the center or nearer the surface. It has a uniform density.
This is not true of our infinite saddlem. Look at the one you made. Remember as you were making it, how it was binding up at the center. This is because there was more paper trying to fit into a smaller space than at the outside. Well the same would be true of our infinite saddle. It would have a density gradient. It would be heavier at the center than near the surface. In nature several objects exhibit this density gradient. Our earth, moon and sun are among them. I am not saying that these natural objects are saddles. I am saying that if you compare them to infinite saddlems it will be more realistic than comparing them to simple, geometric spheres.
The saddlem also has some things to teach us about the smallest things in the universe, the subatomic particles. Take the 1080 saddle you made and a pair of scissors. Pick any spot along the outer edge and cut inward toward the center. Make your cut about an inch or so. Then turn your scissors and cut at a right angle. Trim parallel to the edge about an inch inwards. You can cut one way or the other. You are cutting a ribbon from the edge of the saddle. It is not important that your ribbon is an inch thick.

Trim until you come all the way back to your starting point. You have done two things: First, you have made the saddle smaller. Second, you have made an entirely different form, a helix. We can think of a helix as an unbound saddlem.
The DNA molecule carries the code of each living organism within each cell. It takes the form of a double helix. The orbit of our planet about the sun is helical. This is because the sun also moves through space as we are going around it. When seen from outside of our solar system, the earth would appear to follow a path like a wobbly coil spring.

FIGURE 7
Now let's demonstrate that the saddlem has two forms, bound and unbound. Cut another ribbon from your saddle. This time don't start by cutting inward from the edge. Instead make a small hole about an inch or so inward from the edge. Please work safely. Then just start cutting parallel to the edge as you did before, like you were trimming off the brim of a hat. When you are finished your helix will be connected in a circular manner.
Imagine what this process would be like on an infinite saddlem. Think of it occurring in both directions. You have seen the ribbon falling from the saddlem. Now, close your eyes. Can you see the saddlem forming from the ribbon? At this point it may be helpful to remember that our little model is made from paper. Its dimensions don't relate to anything in particular. It is just a way to help you see the process. The ribbons could be thinner than your hair and wind out to the moon. No one knows for sure how protons and electrons gain and lose energy, but they do. Sub-atomic particles give up energy and take it in as they jump from one state to the next. They seem at one time to be a particle and at others to be a wave. This little trick of ours is a nice way to visualize that happening.
Every age, including ours, has a view of the universe - the current best guess of what makes it all tick. That view, whether or not it is obvious to the majority of the people, is rooted in geometry. In other words we cannot possess a concept of the nature of reality that transcends our geometrical understanding. One reason that knowledge today is somewhat adrift is that we are trying to deal with quarks using Platonic understanding. The licosas offers an another viewpoint. It says that the phenomenon we observe can be explained within a system of geometry that takes another approach. Classical geometry is not dismissed, but is regarded as the product of harmonics within the licosas. (See the Dimension series.)
GLOSSARY
All text and illustrations copyright 2001, J. M. Mongan, Oak Park, Michigan USA This material may be used in classrooms for educational purposes. This text and these illustrations may not be used in any for profit enterprise without the express permission of the author.