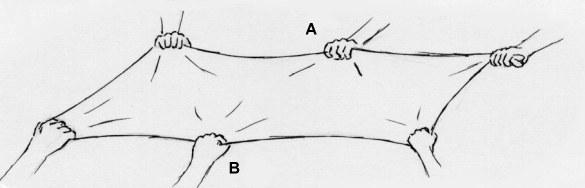
Instruct A to take his free hand and make the thumbs-up sign. Then place his thumb under the middle of the blanket and push up enough to make a small mound. Instruct B to place the fingers of his free hand, pointing downward, on top of the blanket gently surrounding A's thumb. All the while the blanket is being kept taut.
Now we will demonstrate that this distortion in the blanket can move around without affecting the blanket. Instruct A and B to move together horizontally around the blanket. Note how the mound in the blanket, a local distortion, can move about.
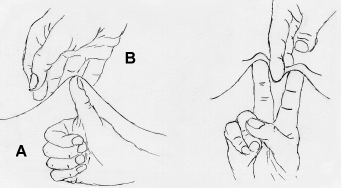
Next, instruct B to pinch the blanket between his fingers (and A of course to get his fingers out of the way). Then tell B to twist the blanket as much as he can.
Solicit two observations:
First, the twist pulls against the corner people and A and B's grasping hands. Does it pull harder for the corner people or for A?
Second, could this twist roam about the blanket as we demonstrated for the mound? Sure, if it could perserve its form as the blanket flowed around it. A and B showed by preserving the mound shape how the blanket "flowed". You may also try to move a twist around by having A and B make "v for victory" signs in opposing directions.
Third, have A help each of the corner students to each make their own twists. Note that the closer the twists are to each other, the greater the strain on the cloth between them. Would this strain be inversely proportional to the distance?
Presumably you have introduced your students to the saddle and the concept of the infinite saddle. As we twisted up our paper circles we noted that the upper limit would be a sphere. We also noted that the paper circles we used could have any radius. These are simply three inch radius because its a convenient size to work with. They could have an infinite radius. Let's subtract their thickness and say they are two dimensional, plane circles of infinite radius. We could then have a bound helix of infinite degrees but no thickness. That's because we can heap all the two dimensional planes on top of each other that we want. Do you see what's comming next, the saddle being formed from the twisted two dimensional "beach blanket". The saddle could also move about the blanket as a topological feature.
Let us say for arguments sake that we have described a primary particle. We see its twistedness as the foundation of three dimensional physical structure (refer to density gradient) and its sheetness as two dimensional. Wait, you say, an electron emits a photon in all directions. How can this be two dimensional? Refer back to matter - energy to see how our saddle can peel off a shell in all directions at once.
Back to gravity, as each student put his or her own twist to the blanket, tension developed between the twists, greater as they became closer. What if these twists were able to pack up adjacent to each other? Let's say B's is a central twist surrounded by six other twists who moved up around it. Originally, when they were separate, they each exerted their own tugs. Now that B's twist is surrounded, does that mean that it's tug disappeared? No, it is still there, just displaced. With all these twists piling up, it cumulates. Many together would exert strong tugs able to act at great distances, like gravity does. If we had more people available we could use a parachute and have a dozen holding the perimeter and another dozen making twists.