What then is the nature of a plane that is not flat, what dimension is it? You have already seen a planar system that is between dimensions, it is described in UU Basics, elsewhere on this site. It is shown that a two dimensional plane can be driven to occupy all the points in a three dimensional space. It is space filling. That I have called the "saddlemniscus" or "saddlem". It is composed of straight lines radiating from a point center to form a plane surface. As more surface is added, it occupies more space. Yet it has only the thickness of a point. We have shown that it is a part of a series that runs from line through cone to sphere. So, any saddlem that we make will be some fraction of the way from flat circle to sphere. It will lie between the second and third dimensions.
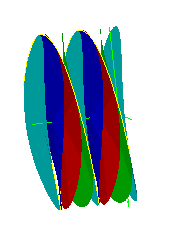
A saddlem has both amplitude (height) and frequency (number of humps). If you performed the exercises, the saddlem you made has two high points and two low ones - the maxima and minima. That is because it has a frequency of two. (A saddlem of frequency three would have three maxima and three minima and so forth.) As the amplitude of your model grows, you reach a special harmonic point. There, for any given radius, the maxima and minima are all exactly equidistant from each other. This is also true of a regular tetrahedron, each vertex is equidistant from the others. The center of the tetrahedron occupies the center of the saddlemniscus. That match is shown on the homepage of this website and is also illustrated here. I call this harmonic relationship the "tetrahedral saddlemniscus", the abbreviation St is used here to refer to it. No, it is not being given sainthood, it should be capital S with a subscript t. Some browsers still have problems with subscripts and to avoid confusion, a simple St will have to do. Besides I'm too lazy to keep typing out tetrahedral saddlemniscus.
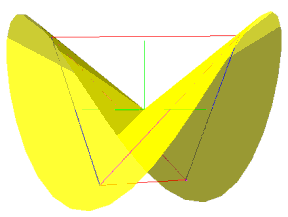
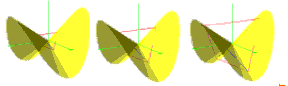
Illustration 1 TETRAHEDRON DEFINED BY A SADDLEMNISCUS
All saddlem are composed of straight lines. Radii of the same length from the center to the high and low points will define the vertices of a tetrahedron. Take half of that radius, those maxima and minima will also define a tetrahedron (just a smaller one). So will one third. So will any radius. Remember that the saddlem has no natural limit to its radial length. It has an infinite radius. Thus, one saddlem can define an infinite number of tetrahedra. They would all share the same center and orientation in space. The next illustration shows this relationship for three different radii on a single saddlem.
This illustration (and all that follow) is also a link to an animation showing the process as a smooth flow. Both the illustrations and the animations are in the form of Quicktime Movies, .mov extension. I have attempted to keep the file sizes manageable for most users so that downloads are not too slow, just click on the picture and the animation will launch.
Illustration 2. SEVERAL TETRAHEDRA DEFINED
Click picture for movie
Click "BACK" to return
What you are seeing is a series of three dimensional figures defined by a single fractional dimensional figure. The lower limit of the series is a point and its upper is an infinitely large tetrahedron. The edges of a tetrahedron are "short circuits" across the St maxima and minima. Planes formed by these edges are easily seen by dunking a wireframe model of a tetrahedron in a soap solution. The illustrated process for building a regular tetrahedron is given in the article "How to Build a Tetrahedron" on this website. The planes of the soap bubbles are composed of these short circuits. A solution for soap bubbles is described at the end of that article.
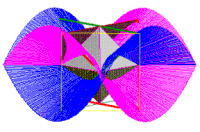
You may remember from DIMENSION Part 1 that we showed how two tetrahedra define a cube and its double, the octahedron. That is still true. The St also has a double - the negative of its function. The saddlems each define their own tetrahedral series. One St is shown in blue and its double in magenta. They are are more than simply duals, like the octahedron and cube. With duals, the vertex of one occupies the center of a face of the other. These St are cojoined, a radial line from the edge of one to the center does not stop there. It continues on through the center to become a line of the other. More simply put, a maximal line on the blue becomes a minimal line on the magenta. It may be easiest to see at the nodes where the two intersect. The line on the illustration defined by the intersection of the blue and magenta continues through the center to the opposite node. It can be seen as a horizontal line. Remember that these are in the same family as cones. Cones can be generated by an infinite line rotating about a point. So are saddlem, only the line follows a wobbly path instead of a circular one.
Illustration 3 DUAL SADDLEM WITH SHORT CIRCUITS
Click picture for movie
Click "BACK" to return
What you have seen thus far is a small fraction of the whole system. Look at the blue St, you will notice that line across the two maxima doesn't penetrate that saddlem. That is true of all edges which short circuit across two maxima or two minima, they are free. The other four edges run from a maximum point to a minimum point, all cutting through the plane of the St. A tetrahedron can be viewed as pairs of edges. The pairs are opposite from each other across the figure. They are color coded by pairs in the first illustration. There are three sets of two each. One set does not penetrate - in the first illustration it is the red pair setting horizontally. It could be either one of the other two sets. By rotating our saddlem over and around, we could make the free pair either of the other two colors. The point is, one tetrahedron can be defined in this manner by any one of these three sister saddlem. Here is an illustration and movie of the three.
Illustration 4 THE THREE SISTER SADDLEMS
Click picture for movie
Click "BACK" to return
An St is simply a harmonic point in the saddling process. The lower limit is a line and the upper is a sphere. Remember that if we could add an infinite number of circles to our saddlemaking, we would wind up with a sphere. Every point on the surface would be covered by some point on the edge of some circle. Since we are discussing regular tetrahedra, they can be circumscribed by a sphere. There is no one magic tetrahedron, there are many. We can choose any one to be the focus of this discussion. What we have done so far is to give you a way to visualize a larger process. That process is how, I believe, different dimensions relate.
MATTER AND ENERGY Part 2
If you have read the matter-energy article, you may have bristled at my statement that "Energy is a two dimensional phenomonon as viewed from a three dimensional platform". Now we have a way to illustrate that.
We are going to suppose that a regular tetrahedron represents a subatomic particle. Not one in particular, just a general one. It will be considered the basic building block for matter. Its attendant saddlem will represent energy. I propose that as the tetrahedron shrinks, its matterness reverts to two dimensional energyness. In the physical universe this could be the emission of a photon. Let's look at it through our harmonic model.
Illustration 5 CONVERTING THE THREE DIMENSIONAL INTO TWO
Click picture for movie
Click "BACK" to return
*Hipnote (like a footnote only not at the bottom): This article is my first to use animations generated by mathematical equations. It does not negate the previous work with paper circles. There is only so much a paper model can reveal. In Matter-Energy and Photon in a Fishbowl, I described tearing off the edges of the saddlem to model a process. But now we see that physical separation is not necessary. The animations offer a theoretical structure for the exchange between matter and energy. Tearing paper is used as a practical way to demonstrate concepts that would otherwise get tangled in a purely verbal description.
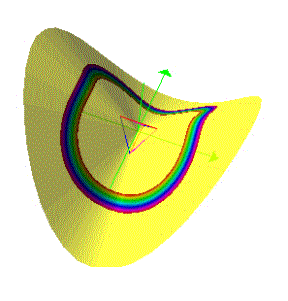
In Photon in a Fishbowl I wrote, "That means there is a zero boundary (modulus) at some radial distance from the center which lies between the two and is neither." The wave you see spreading out begins at that zero modulus. The change in size of the tetrahedron is the response, restabilizing the particle with a new balance. As the saddlem is two+ dimensional and the tetrahedron is three dimensional, so do we represent the boundary of matter in a two+ dimensional field. As our paper saddlems were twisted, we imparted energy to it. So a two dimensional plane is distorted into a sphere with an infinitely dense, point center. What we have been examining occurs around that point center. Conversely, the sphere's extent is limitless. Comprehend, if you will, superclusters of galaxies and all the point centers that would be represented for all of the particles. Each point is center for a limitless, space filling veil of a saddlem.
The process works in reverse also. As an energy wave comes in and strikes our tetrahedron, it pops up an energy level absorbing a "photon". The animation shows it as a wave on the surface of the St. St's are based on sine or cosine functions. Their doubles are their negatives. So for each + sine based St and its - sine double, we have a couple of +/- cosine cousins. The next illustration shows the same process for +/- sine/cosine, the amplitude of the wave has been allowed to grow to better show its spherical form. The sister functions are not shown.
Illustration 6 ABSORBING ENERGY
Click picture for movie
Click "BACK" to return
Saddlems also have a handedness. You may have noticed while building the Basic UU models that, like springs, they can be wound dextro or levo (right or left). So we can consider them to have a spin built in. There is also an opposite handed set to all we have revealed.
Since the saddlem is infinite in radius and spherical, this ripple could travel across the universe. Imagine this happening on a distant star. It would reach us on a two dimensional plane that we view edge on. If it strikes matter, like a cell in our eye, it would impart its energy into 3d-ness. Since the veil of It is space filling, we see it from any direction. This is the same as the absorption process we reviewed. Instead of happening to our parent particle, it happens to another one. They each have different centers but are connected by a line. So their saddlems have a radial line in common. Which leads us to electricity.
ELECTRICITY
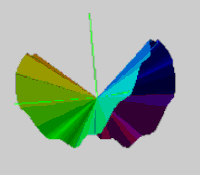
We have been using an St to model the process of a particle receiving or getting rid of energy. In this system, the 2 dimensional and 3 dimensional are allowed to transform into each other. We have shown how it can radiate outwards in an expanding shell. Let's take a look at another way the St can disperse extra energy. It has a second pathway, similar to the ringing of a bell. When a bell is struck, there is nowhere for the energy to go beyond the bell itself. So the bell starts vibrating to dissipate it. The bell is heard to ring as the excess energy pulses the air around it. Well, I believe the St can do the same thing - geometrically speaking. The solid "particle" can exchange some of its 3d-ness with the 2d saddlem by inducing it to distort. Its normally smooth appearance becomes jagged. Its average form is the same but its actual form has a subharmonic on it.
Illustration 7 BELL RINGING ENERGY DISSIPATION
Click picture for movie
Click "BACK" to return
Way back in Dimension Part 1 we showed how the tetrahedron and cube are fractal. A tetrahedron is composed of smaller tetrahedra, and so on. If we put a bunch of cubes together like building blocks, we would have a 3d lattice of these. With what we have learned above, we can plug an St into the center of each of the possible tetrahedra. If we were able to set one "ringing", it could set the others "ringing". It would set up a chain reation throughout the lattice. Now let's say we make our lattice long and thin. We start vibrating one end. The vibration will travel through the lattice until it reaches the other end. In a perfect system with no losses, it would continue vibrating until it finds something to accept the excess energy. So if our lattice represents copper wire and we induce all the little saddlem at one end to vibrate in this manner, that would travel along the wire to the other end. If it finds a light bulb there, it will dissipate its energy by heating the filament and emitting photons as light. Neat, eh?
What about all the St that are up against the outer wall of the wire. They make up the outer shell of the lattice. Some of the saddlems will be perpendicular to the wire. The wire would follow the z axis in our illustrations. They still radiate in the fashion we first discussed (Illustration 6). It will radiate outwards from the wire. Say we have a flow of current through the wire which lights a bulb and then goes to the ground. The flow of the bell ringing will not be enough to get rid of all the energy. So the system will try to radiate it away. This creates a field around the wire running along its length. It is still a 2d+ phenomenon. It will not be able to interact with the 3d world until it finds an acceptable receiver to take the energy in. This is how I view electromagnetism in terms of the saddlemniscus.
If more electricity is being drawn through the wire than the radial and bell energy can handle, it will convert to heat. That is what happens in a short circuit. The atoms of the wire start to vibrate to relieve the extra tension. The insulation can melt and nearby objects can be heated to the point of combustion.
Illustration 8 THE ELECTROMAGNETIC FIELD
Click picture for movie
Click "BACK" to return
That is the short of it. Please excuse the mixing of metaphores between the theorectical construct of the saddlemniscus and the real world of the copper wire. This is an article for the web and I have tried to keep it short and to the point. I hope you are able to separate the parts that are my theory from the accepted versions. The saddlemniscus is my creation. I offer it as a way to explain these processes. I think the real world works in some similar fashion. You can always email me if you have questions. The illustrations and movies have been compressed to speed up downloading on the web. That has a cost in sharpness. I plan to offer a CD in the future with more detail, equations and clearer illustrations.
All images are generated by equations using Pacific Tech's Graphing Calculator except numbers 4.3 and 4.4. They were drawn using Vectorworks 3D CAD system.