To perform this exercise, you will need a six inch diameter spherical fishbowl. These are available in clear plastic for a very modest cost ($3 plus). I have found them in pet supply stores. The six inch diameter is needed because the paper circles we will be using are the same size.
First construct a saddle of six or seven paper circles. Remember that you cannot reverse directions during the taping process. Tape both sides of the joining seams. When your stack is complete, trace the outer edge with your finger. It should follow a smooth helix either right or left, but not both. Now wind it up into a saddle in the manner described in the kit. Proceed to remove the edge as a continuous ribbon (figure 10 in the book or see the website). If it breaks, tape it together again. You may also staple across the seams where circles join for added reinforcement. Width of the ribbon should be about an inch or about a third of the radius, you need not be precise.
NOTE:DNA DEMONSTRATION uses the continuous ribbon you now hold in your hands. So you may want to keep track of this proceedure (and ribbon) for that exercise.
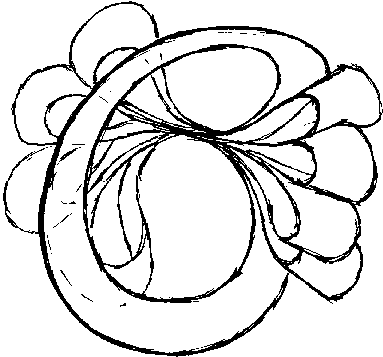Illustration 1, The Bowtie
Carefully fold the ribbon as if you were making a bow for a present, pinching it between your fingers - illustration 1. Notice that you have an arch remaining that goes over the top. It may appear slightly different depending upon whether you started with an odd or even number of paper circles. Holding it by the center, insert it into the fishbowl. Release it. Spread it out inside of the fishbowl. The paper ribbon has an outer (original) edge and inner (torn or cut) edge. The outer edge of the paper should touch the inner wall of the fishbowl. It will appear similar to illustration 2. What you have done is to subtract the inner part of the saddle. The fishbowl simply supports the structure and aids with visualization of the ensuing process.
From previous work, you will remember that in our view the saddle you made lies along a continuum that goes from line through cone to circle and then sphere. The upper limit of our process is a saddle made from an infinite number of circles. It would be spherical and have a continuous surface. By that I mean some point from the edge of some circle would occupy each point on the surface. It would have a density gradient toward the center and the center would be an infinitely dense point. This is what is meant by an infinite saddle.
When you were winding up the taped circles into the saddle, you applied force to do so. Had you let go or if it slipped from your fingers, you would have seen it snap back. It wants to return to its lower energy state. However we have compelled it into a higher energy state with our trusty cellophane tape. This means that the outer portion is in compression. You may also have observed small tears developing at the center. This is because it is in tension. (Circles from Mē Solids have a small hole at the center to alleviate this problem.) So, our model is stressed between inner tension and outer compression. That means there is a zero boundary at some radial distance from the center which lies between the two and is neither. Assume for the sake of argument that this zero modulus is where you tore the ribbon.
In our infinite saddle, a jolt of some kind may cause the model to shear at this boundary. The ribbon would separate from the core. It would resemble the rind of an orange separated from the meat but still continuous. That is how you should visualize your ribbon in the fishbowl, the outer rind of an infinite saddle with the center removed. The rind is composed of our two dimensional ribbon. Once this jolt has created the shear, what happens to the remaining sphere, the juicy part or meat of our orange? It simply restabilizes into another tension-compression pair with a new zero modulus at a smaller radius. If it were to receive another jolt, it could reseparate into another rind-meat pair and so on.
What interests us now is what we have in our fishbowl, the rind of a subatomic particle, a photon. Now imagine our fishbowl to vanish as if it were made from a frozen soap bubble that suddenly popped. The ribbon was the compression part of our earlier pair. Now that the restraint of the outer shell is gone, it wants to decompress. It will do so by expanding outwards in all directions at once like a balloon released into a vacuum. Or more to the point, like a photon of light emitted by an electron.
Illustration 2, Photon in a Fishbowl
"Wait", you say, "there's a problem". The photon will go off in all directions. I would be able to observe it no matter what my location. Its wave front would be continuous regardless of radius. But your model in the fishbowl would not. Even if it were infinite in degrees, gaps would form between the sheets as it grew ever larger in expansion. There are two possible answers. First, the sheets could become thicker. But from the beginning we have considered our saddles to be composed of two dimensional sheets. So we can't get any thicker and stay within our system. But we still have a way out. We can sacrifice the width of our ribbon to its length-like a rubber band when stretched. Width here refers to the width of the ribbon we tore from our original saddle, the inch or so. Length is the brim length, the distance around its outer edge. Thus as the radius of our rind expands, the brim length of the ribbon expands also to keep the surface whole. If this is so where does the process end? It would end when our ribbon has been reduced to a one dimensional string. It also occurs at a speed fast enough to allow the wave front -represented by the outer skin of the rind- to travel at the speed of light and stay a continuous shell. The amplitude of the photon, essentially how much energy it carries, is represented at any time by the width of the ribbon.
At this point it may be useful to interject that this model uses circles, but nature doesn't seem to. Nature favors ellipses. It would be unduly complex to make our saddles from ellipses sharing a common foci. In a more perfect description of a particle, I would picture its point center orbiting between foci within a small shell.
As they stand, saddles do not have a stable configuration. As you hold one in your hands, you can twist it into a variety of balances. In some, more of the circles seem to bunch around an equator. In others, the circles distribute themselves more evenly. In comparing the infinite saddle to an electron I envision the whole thing squirming around before a photon breaks loose. Thus the photon itself would be in a more a dynamic condition than our mild mannered fishbowl suggests. It would I believe be ringing. This ringing is the source of what we perceive as color. Is it ringing like a bell? A bell rings because its surface is mechanically joined. Thus a jolt which distorts it will cause the entire body to seek restabilization while dissipating the energy of the strike. This is different. If we can imagine striking our fishy photon, it would not act with the connectedness of a bell. It is, after all, a folded ribbon.
Yet, the ribbon could still vibrate in a uniform manner. Let's say the ribbon in our photon is vibrating in a particular shade of green. As the rind expands it eventually strikes an object, a pure green leaf of the same shade. Actually only a leaf shaped portion of it strikes and the rest keeps going. It would be as if the ribbon shears off at the leaf-non leaf boundary. That which remains behind imparts its energy to the leaf as in the warming effects of sunshine. It also imparts its vibration, as a tuning fork when placed next to another tuning fork of the same note. The leaf which has been struck is thus set to vibrating and emits green, because that is its natural harmonic. If our photon had been red, it would not. The energy of the part of the photon striking the leaf would be absorbed as heat.
What about the rest of the photon, the one with the leaf shaped hole in it? It would still be expanding, relieving its compression. The hole is what we call a shadow. As the rind expands in its outward journey, so does the shadow.
Up until now we have been considering only a single photon. But our real life experience comes from multiple photons, emitted one after the other in a steady stream. From the sun, the radius of each is so large that they appear as flat as a wall. That seems to us as a continuous source of light. It seems almost liquid like and exhibits the properties of waves. But as we have seen, it can impact other objects as though they have been struck with a particle. This is the dual wave-particle nature of light as explained by the photon in a fishbowl.