Three dimensions can only describe so much. They are simply a convenience for describing objects in our world. They are more effective than two dimensions in some regards but still leave a lot out. Time, heat, potential and kinetic energy are examples that come to mind. I cannot accurately describe the motion of an object through space unless I arbitrarily choose some center of the universe. It is entirely a mental process. Other people may or may not agree with me depending on how well our common concepts match. I may say, "It is a hundred and twenty miles to your house". You might reply, "No, it is 193 kilometers". Somewhere in our heads we generally seem to be able to suspend apparent reality and look at the world as if plane geometry is true. Well, it is as true as solid geometry is. We have set up a bunch of rules which are consistant in themselves, our formulae and calculations pretty well work out and we come up with some neat stuff.
It does however go on inside of our heads. That is a nebulous region where a bunch of brain cells exchange energy in some fashion and thoughts exist. Thoughts are mysterious, like being aware is mysterious. I do not pretend to know how it happens or what it is. I do know that we get ourselves into a lot of trouble confusing reality with our mental image of reality. Then, that is also how we accomplish a lot of the wonderful things we do. Somehow we are able to construct within our minds shorthand versions of the world our senses perceive. Where it gets really interesting is that we are are able to manipulate and deduce relations between these shorthand versions that shows us a path to manipulating things in the real world around us. The deciphering of the structure of the DNA molecule and the subsequent development of the ability to genetically modify organisms strikes me as a prime example.
What we have been investigating in this series is a direct relationship in the real world of geometry to the shorthand world of our minds. Specifically, that two dimensional figures spawn three dimensional counterparts. One presents a map to the other. Let us continue with the final of the Pythagorean solids, the icosahedron. We showed that the decagon spawned the dodecahedron in Dimensions Part 2. The drawing that we used contained an inner decagon. We are now going to jump a level and place the dodecahedron at the inner decagon.
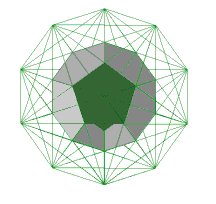
You may also recall in the last exciting episode, the figure called the pentagonogram. It showed the relationship between the pentagon and the five pointed star-the pentagram. We are now going to express that relationship on one face of the dodecahedron. The process of stellation means to take a plane figure and extend its sides. Doing that all around will draw a star on a regular figure. Trace out a set of the D¢10 chords (there are two sets) and you will see that they not only describe the darker pentagon in the center but they also describe its matching star.
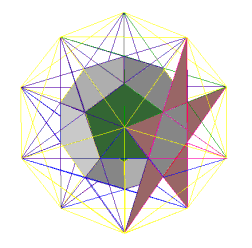
We placed a three dimensional dodecahedron within a two dimensional decagon. We have stellated a different face and now it appears that our two dimensional star, on top of a flat face of the solid, corresponds to the chords of the decagon. Pretty neat, huh? But wait, that's not all. If we can do this to one face, we can do it to all faces. We will begin not as you may suspect, by stellating another face. To demonstrate where the process is leading, we will selectively extend a few lines.
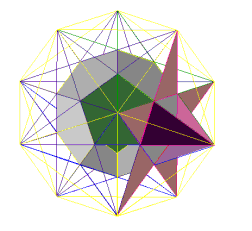
As you can see, we are creating a prism on the stellated face. (If you have access to 3d viewing software, models are provided.) The figure requires nothing more than choosing correct chords. We are still able to do all we need using only the chords of the decagon. Obviously this process can be continued on any face.
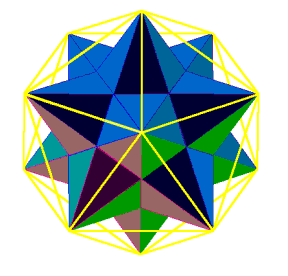
This model is presented with one stellation at the center pentagon, its tip pointing at you. Notice in figure 4 that we have also identified a series of triangles. These are the leftovers from our excercise. They connect the 3d stellar points of our dodecahedron. They describe the fifth and final Platonic Solid, the regular icoshedron. It consists of twenty faces, each of which is an equilateral triangle and twelve vertices. It is the double of the dodecahedron. Since it is a solid figure it can be rotated.
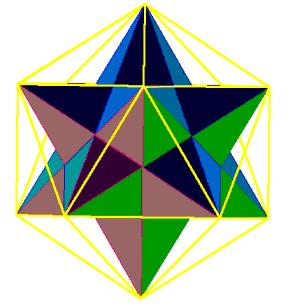
Here is another view of it, rotated to bring an equilateral triangular face square to the front. Could the icoshedron be stellated? Of course, since it is doubled with the dodecahedron, that is what it will produce, as that is what produced it. This view is presented to show an old friend returned, the hexagon from Dimension Part 1. It could again be used to demonstrate the cube. So we have now gone full circle, back to where we began. Classical geometry had a special regard for the figures which could be constructed using only a compass and straight edge. That was the most accurate construction method available in ancient times. In theory it is perfect. All of the above figures can be constructed with a compass and straightedge. You need to decide what radius to begin with and call the unit. It could be an inch, a meter or a mile, everything will still work out.
In ancient times there was a special regard for ratio. Empires could come and go, the stars change their positions over centuries, but one half is always one half. The perfection that mankind has generally reserved for the divine can be constructed and seen and felt within these five regular figures. Geometry is as close to touching the face of God as I hope to achieve.

Are we finished? No, we have yet to tie all of this to the Unit of the Universe. That will be the subject of our next exciting episode, Dimension Part 4.
Copyright 2000, Mike Mongan, Oak Park MI